
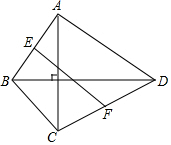
 在四边形ABCD中,对角线AC⊥BD且AC=4、BD=6.E、F分别是边AB、CD的中点,则EF=$\sqrt{13}$.
在四边形ABCD中,对角线AC⊥BD且AC=4、BD=6.E、F分别是边AB、CD的中点,则EF=$\sqrt{13}$. 分析 取BC的中点G,连接EG、FG,根据三角形的中位线平行于第三边并且等于第三边的一半求出EG、FG,并求出EG⊥FG,然后利用勾股定理列式计算即可得解.
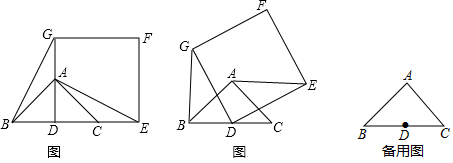
解答 解:如图,取BC的中点G,连接EG、FG,
∵E、F分别是边AB、CD的中点,
∴EG∥AC且EG=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2,FG∥BD且FG=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3,
∵AC⊥BD,
∴EG⊥FG,
∴EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,勾股定理的应用,作辅助线构造出直角三角形是解题的关键.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
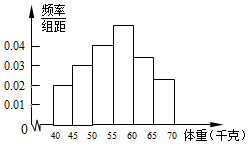 为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.
为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com