
【题目】如图,在平面直角坐标系xOy中,一次函数y=-x+b的图象与反比例函数y=-![]() 的图象交于点A(-4,a)和B(1,m).
的图象交于点A(-4,a)和B(1,m).
(1)求b的值和点B的坐标;
(2)如果P(n,0)是x轴上一点,过点P作x轴垂线,交一次函数于点M,交反比例函数于点N,当点M在点N上方时,直接写出n的取值范围.

【答案】(1)b的值为-3,点B的坐标为(1,-4);(2)n<-4或0<n<1
【解析】
(1)将A(-4,a)和B(1,m)代入数y=-![]() ,可求a、m的值,即可求得B的坐标,然后利用待定系数法即可求得b;
,可求a、m的值,即可求得B的坐标,然后利用待定系数法即可求得b;
(2)由图象结合A、B的坐标直接得到.
解:(1)∵反比例函数y=-![]() 的图象经过点A(-4,a)和B(1,m).
的图象经过点A(-4,a)和B(1,m).
∴-4a=-4,m=-4,
∴a=1,m=-4,
∴A(-4,1),B(1,-4),
∵一次函数y=-x+b的图象经过B(1,-4),
∴-1+b=-4,求得b=-3;
故b的值为-3点B的坐标为(1,-4);
(2)∵A(-4,1),B(1,-4),
∴由图象可知,当n<-4或0<n<1,点M在点N上方.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1、x2,那么x1+x2=-p,x1·x2=q.请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+mx+n=0 (n≠0),求出一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知a、b满足a2-15a-5=0,b2-15b-5=0,求![]() 的值;
的值;
(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
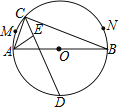
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过点A(3,1)和点B(0,-2),
(1)求一次函数的表达式;
(2)若点C在y轴上,且S△ABC=2S△AOB,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
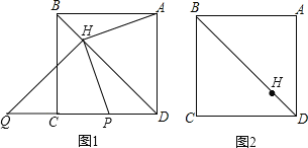
【题目】 已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.
(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是______.
(2)当H点运动到图2所示位置时
①依据题意补全图形.
②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.
(3)若正方形边长为![]() ,∠PHD=30°,直接写出PC长.
,∠PHD=30°,直接写出PC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
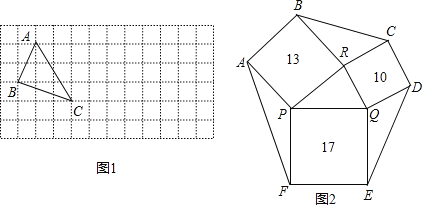
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
(1)△ABC的面积为: _________ ;
(2)若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积;
,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积;
(3)如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13,10,17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com