

分析 (1)根据两家超市的优惠方案,可知当一次性购物标价总额是300元时,甲超市实付款=购物标价×0.88,乙超市实付款=300×0.9,分别计算即可;
(2)设当标价总额是x元时,甲、乙超市实付款一样.根据甲超市实付款=乙超市实付款列出方程,求解即可;
(3)首先计算出两次购物标价,然后根据优惠方案即可求解.
解答 解:(1)当一次性购物标价总额是300元时,
甲超市实付款=300×0.88=264(元),
乙超市实付款=300×0.9=270(元);
(2)设当标价总额是x元时,甲、乙超市实付款一样.
当一次性购物标价总额是500元时,
甲超市实付款=500×0.88=440(元),乙超市实付款=500×0.9=450(元),
∵440<450,
∴x>500.
根据题意得0.88x=500×0.9+0.8(x-500),
解得x=625.
答:当标价总额是625元时,甲、乙超市实付款一样;
(3)小王两次到乙超市分别购物付款198元和466元,
第一次购物付款198元,购物标价可能是198元,也可能是198÷0.9=220元,
第二次购物付款466元,购物标价是(466-450)÷0.8+500=520元,
两次购物标价之后是198+520=718元,或220+520=740元.
若他只去一次该超市购买同样多的商品,实付款500×0.9+0.8(718-500)=624.4元,或500×0.9+0.8(740-500)=642元,
可以节省198+466-624.4=39.6元,或198+466-642=22元.
答:若他只去一次该超市购买同样多的商品,可以节省39.6或22元.
点评 本题考查了一元一次方程的应用,理解两家超市的优惠方案,进行分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
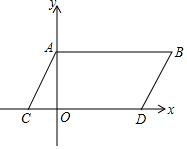 如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a-3)2+|b-5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
如图,在平面直角坐标系中,点A,B坐标分别为A(0,a),B(b,a),且实数a,b满足(a-3)2+|b-5|=0,现同时将点A,B分别向下平移3个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题再现:
问题再现:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
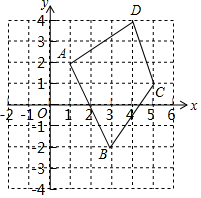 如图所示的直角坐标系中,四边形ABCD的四个顶点的坐标分别是:A(1,2),B(3,-2),C(5,1),D(4,4)
如图所示的直角坐标系中,四边形ABCD的四个顶点的坐标分别是:A(1,2),B(3,-2),C(5,1),D(4,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com