
 如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,BD和CD交于点D.
如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,BD和CD交于点D.分析 (1)先根据角平分线定义得到∠ACE=2∠1,∠ABC=2∠2,再根据三角形外角性质得∠ACE=∠ABC+∠A,则2∠1=2∠2+∠A,接着再根据三角形外角性质得∠1=∠2+∠D,易得∠A=2∠D,即∠D=$\frac{1}{2}$∠A,进而得出答案;
(2)先根据角平分线定义得到∠ACE=2∠1,∠ABC=2∠2,再根据三角形外角性质得∠ACE=∠ABC+∠A,则2∠1=2∠2+∠A,接着再根据三角形外角性质得∠1=∠2+∠D,易得∠A=2∠D,即∠D=$\frac{1}{2}$∠A,进而得出答案.
解答 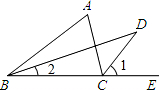 解:如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
解:如图,∵BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴∠ACE=2∠1,∠ABC=2∠2,
∵∠ACE=∠ABC+∠A,
∴2∠1=2∠2+∠A,
而∠1=∠2+∠D,
∴2∠1=2∠2+2∠D,
∴∠A=2∠D,
即∠D=$\frac{1}{2}$∠A,
(1)当∠A=40°,则∠D=20°;
(2)若∠A=90°,则∠D=45°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.主要用在求三角形中角的度数:①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了三角形外角性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,FG⊥AE于G,EH⊥AF于H.连接AC、EF、AM,AC=20,EF=16.
已知如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,FG⊥AE于G,EH⊥AF于H.连接AC、EF、AM,AC=20,EF=16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com