
已知:如图,△ABD中,AC⊥BD于C, ,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.
,E是AB的中点,tanD=2,CE=1,求sin∠ECB和AD的长.

科目:初中数学 来源:2014-2015学年北京市燕山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,点A,B,C的坐标分别为(0,1),(1,-1),(5,1).

(1)直接写出点B关于原点的对称点D的坐标;
(2)将△ABC绕点C顺时针旋转90º得到△A1B1C.请在网格中画出△A1B1C,并直接写出点A1和B1的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市顺义区九年级上学期期末考试数学试卷(解析版) 题型:填空题
阅读下列材料:小华遇到这样一个问题:已知:如图1,在△ABC中,AB= ,AC=
,AC= ,BC=2三边的长分别为,求∠A的正切值.
,BC=2三边的长分别为,求∠A的正切值.

小华是这样解决问题的:如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.
(1)图2中与 相等的角为 ,
相等的角为 ,  的正切值为 ;
的正切值为 ;
(2)参考小华解决问题的方法,利用图4中的正方形网格(每个小正方形的边长均为1)解决问题:如图3,在△GHK中,HK=2,HG= ,KG=
,KG= ,延长HK,求
,延长HK,求 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数 在
在 与
与 的函数值相等.
的函数值相等.
(1)求二次函数的解析式;
(2)若二次函数的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,一次函数 经过B,C两点,求一次函数的表达式;
经过B,C两点,求一次函数的表达式;
(3)在(2)的条件下,过动点 作直线
作直线 //x轴,其中
//x轴,其中 .将二次函数图象在直线
.将二次函数图象在直线 下方的部分沿直线
下方的部分沿直线 向上翻折,其余部分保持不变,得到一个新图象M.若直线
向上翻折,其余部分保持不变,得到一个新图象M.若直线 与新图象M恰有两个公共点,请直接写出
与新图象M恰有两个公共点,请直接写出 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:选择题
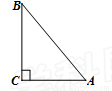
如图,为测学校旗杆的高度,在距旗杆10米的A处,测得旗杆顶部B的仰角为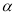 ,则旗杆的高度BC为( )
,则旗杆的高度BC为( )
A.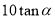 B.
B.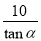 C.
C.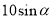 D.
D.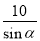
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E.求证:△ACD∽△BCE.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数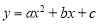 (
(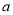 为常数,且
为常数,且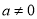 )的图象过点A(0,1),B(1,-2)和点C(-1,6).
)的图象过点A(0,1),B(1,-2)和点C(-1,6).
(1)求二次函数表达式;
(2)若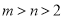 ,比较
,比较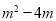 与
与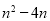 的大小;
的大小;
(3)将抛物线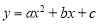 平移,平移后图象的顶点为
平移,平移后图象的顶点为 ,若平移后的抛物线与直线
,若平移后的抛物线与直线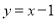 有且只有一个公共点,请用含
有且只有一个公共点,请用含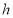 的代数式表示
的代数式表示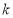 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com