
 如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.分析 (1)根据翻转变换的性质解答;
(2)先根据题意补全图形,根据直角三角形的性质求出BE;
(3)分B是等腰三角形△BEF的顶角顶点、E为等腰三角形△BEF的顶角顶点两种情况,根据等腰三角形的性质、翻转变换的性质计算即可.
解答  解:(1)∵∠OBA=60°,
解:(1)∵∠OBA=60°,
∴∠OAB=30°,
由翻转变换的性质可知,∠BAC=∠OAB=30°,
故答案为:30;
(2)补全图形如图1,
∵BE⊥x轴,
∴∠OBE=90°
∵∠OBA=60°,
∴∠EBA=30°,
∴∠EBA=∠BAC=30°,
∴AE=BE,
∵∠ABC=∠OBA=60°,
∴∠EBC=∠ABC-∠EBA=30°,
又∵∠C=∠FOB=90°,
∴CE=$\frac{1}{2}$BE,
又∵AC=AE+EC=6,
∴AC=BE+$\frac{1}{2}$BE=6,
∴BE=4;
(3)①当B是等腰三角形△BEF的顶角顶点时,如图2,
当BF=BE时,OF=CE=2,
∴t=2÷2=1,
当BF=BE=4时,如图3,
∵AF=AB-BF=4$\sqrt{3}$-4,
∴t=$\frac{OA+OF}{2}$=$\frac{6+4\sqrt{3}-4}{2}$=1+2$\sqrt{3}$,
②当E为等腰三角形△BEF的顶角顶点时,如图4,
∵∠ABE=30°,∠BAC=30°,
则当F运动到A点时,即AE=BE,
∴△BEF为等腰三角形,即t=6÷2=3,
当EF=BE时,由(2)得:AE=BE,
∴EF=AE=4,又∵∠OAE=60°,
∴△AEF为等边三角形,
∴A F=AE=4
∴O F=AO-AF=2,
∴F与图2中F重合,此时 t=1,
所以在点F的运动过程中,当t=1(秒)或t=3(秒)或t=(1+2$\sqrt{3}$)(秒)时,△BEF是以BE为腰的等腰三角形.
点评 本题考查的是等腰三角形的判定和性质、直角三角形的性质、翻转变换的性质,掌握翻转变换的性质、灵活运用分情况讨论思想是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.
如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=120°,则∠D=( )度.| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
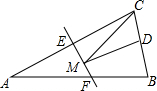 如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为10.
如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A类 | 100 | 30 |
| B类 | 200 | 25 |
| C类 | 500 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.
如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com