

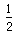 ∠ABC,∠CDF=
∠ABC,∠CDF=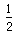 ∠CDA.
∠CDA.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:不详 题型:单选题
 的位置如图所示,点
的位置如图所示,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ;延长
;延长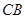 交
交 轴于点
轴于点 ,作正方形
,作正方形 ;延长
;延长 交
交 轴于点
轴于点 ,作正方形
,作正方形 …;按这样的规律进行下去,第
…;按这样的规律进行下去,第 个正方形的面积为
个正方形的面积为
A. | B. |
C. | D.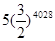 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
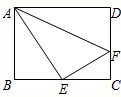
| A.4 | B.6 | C.8 | D.9 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 BFD.
BFD.
| 正方形CEFG的边长 | 1 | 3 | 4 |
 BFD的面积 BFD的面积 | | | |
 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想. 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的平行线交
的平行线交 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
 是
是 的中点;
的中点; ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com