
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
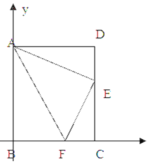
(1)求证:平行四边形ABCD是矩形;
(2)如图2,以点B为坐标原点,水平方向、竖直方向为x轴、y轴建立平面直角坐标系,求直线AF的解析式;
(3)在(2)中的坐标系内是否存在这样的点P,使得以点P、A、E、F为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,直接写出点P的坐标。
【答案】(1)见解析;(2) y=-2x+10 (3)见解析.
【解析】
(1)根据翻折变换的对称性可知AE=AB,在△ADE中,利用勾股定理逆定理证明三角形为直角三角形,再根据有一个角是直角的平行四边形是矩形证明即可;
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算,而后得出F点的坐标,利用待定系数法求解即可;
(3)分三种情况:①当以AE为对角线时;②当以AF为对角线时;③当以EF为对角线时,讨论解答即可.
(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)解:设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
∴F(5,0),易求直线AF的解析式为:y=-2x+10;
(3)如图所示:
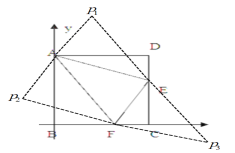
由题意得:A(0,10), E(8,4),F(5,0)
①当以AE为对角线时,
∵四边形AFE![]() 为平行四边形,∴AF=E
为平行四边形,∴AF=E![]() =
=![]() =5
=5![]() ,EF=A
,EF=A![]() =
=![]() ,∵F(5,0),E(8,4),可以看作点F的坐标向右平移3个单位,再向上平移4个单位得到,∴由A(0,10)向右平移3个单位,再向上平移4个单位得到点
,∵F(5,0),E(8,4),可以看作点F的坐标向右平移3个单位,再向上平移4个单位得到,∴由A(0,10)向右平移3个单位,再向上平移4个单位得到点![]() (0+3,10+4),即
(0+3,10+4),即![]() (3,14);
(3,14);
②当以AF为对角线时,
∵四边形AEF![]() 为平行四边形,∴AF=F
为平行四边形,∴AF=F![]() ,EF=A
,EF=A![]() ,∵A(0,10),E(8,4),可以看作点E的坐标向左平移8个单位,向上平移6个单位,得到,∴由F(5,0)向左平移8个单位,再向上平移6个单位得到点
,∵A(0,10),E(8,4),可以看作点E的坐标向左平移8个单位,向上平移6个单位,得到,∴由F(5,0)向左平移8个单位,再向上平移6个单位得到点![]() (5-8,0+6),即
(5-8,0+6),即![]() (-3,6);
(-3,6);
③当以EF为对角线时,
∵四边形AE![]() F为平行四边形,∴AF=F
F为平行四边形,∴AF=F![]() ,AF=E
,AF=E![]() ,∵A(0,10),E(8,4),可以看作点A的坐标向右平移8个单位,再向下平移6个单位得到,∴由F(5,0) 向右平移8个单位,再向下平移6个单位得到点
,∵A(0,10),E(8,4),可以看作点A的坐标向右平移8个单位,再向下平移6个单位得到,∴由F(5,0) 向右平移8个单位,再向下平移6个单位得到点![]() (5+8,0-6),即
(5+8,0-6),即![]() (13,-6);
(13,-6);
综上所述:P1(3,14),P2(-3,6),P3(13,-6)


科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
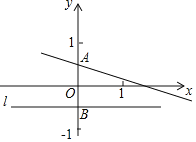
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=12cm,BC=9cm,点D为AB的中点.
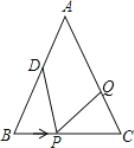
(1)如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,当经过1秒时,△BPD与△CQP是否全等,请判断并说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
(2)若点Q以②的运动速度从点C出发,点P以原来运动速度从点B同时出发,都逆时针沿△ABC的三边运动,求经过多长时间,点P与点Q第一次在△ABC的哪条边上会相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店要进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可完成,需付两组费用共3480元,问:
(1)甲、乙两组工作一天,商店应各付多少元?
(2)已知甲组单独做需12天完成,乙组单独做需24天完成,单独请哪组,商店所付费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
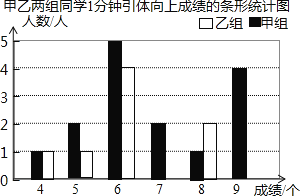
【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
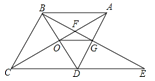
【题目】如图,在菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是( )
①OG=![]() AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
AB;②与△EGD全等的三角形共有5个;③S四边形ODGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。

(1)①求证图1中△ADC≌△CEB;②证明DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)如图所示,现有下列四个结论:①abc>0 ②b2-4ac<0 ③c<4b ④a+b>0.其中正确的结论有( )

A. 1个 B. 3个 C. 2个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com