
【题目】等腰△BCD中,∠DCB=120°,点E满足∠DEC=60°.
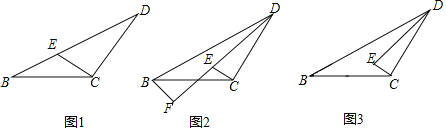
(1)如图1,点E在边BD上时,求证:ED=2BE;
(2)如图2,过点B作DE的垂线交DE的延长线于点F,试探究DE和EF的数量关系,并证明;
(3)若∠DEB=150°,直接写出BE,DE和EC的关系.
【答案】(1)见解析;(2)DE=2EF.理由见解析;(3)BE2=EDEC.理由见解析.
【解析】
(1)先根据等腰三角形性质和三角形外角的性质得:BC=CD和BE=CE,根据三角形的内角和定理证明∠DCE=180°-30°-60°=90°,由直角三角形30度角的性质可得结论.
(2)结论:DE=2EF.如图2中,作DH⊥EC交EC的延长线于H,连接FH.想办法证明DE=2EH,EF=EH即可解决问题.
(3)结论:BE2=EDEC.证明△DEB∽△BEC可得结论.
(1)证明:如图1中,
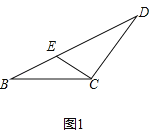
∵等腰△BCD中,∠DCB=120°,
∴BC=CD,
∴∠B=∠D=30°,
∵∠DEC=60°=∠B+∠ECB,
∴∠ECB=30°,
∴BE=CE,
△DEC中,∠DCE=180°﹣30°﹣60°=90°,
∵∠D=30°,
∴ED=2EC,
∴ED=2BE;
(2)解:结论:DE=2EF.
理由:如图2中,作DH⊥EC交EC的延长线于H,连接FH.

∵∠DHE=90°,∠DEH=60°,
∴∠EDH=30°,
∵CD=CB,∠BCD=120°,
∴∠CBD=∠BDC=30°,
∴∠BDC=∠EDH,
∴∠BDF=∠CDH,
∵BF⊥DF,
∴∠BFD=∠H=90°,
∴△DFB∽△DHC,
∴![]() ,
,
∴![]() ,
,
∵∠BDC=∠FDH,
∴△BDC∽△FDH,
∴∠DBC=∠DFH=30°,
∵∠DEH=∠EFH+∠EHF=60°,
∴∠EFH=∠EHF=30°,
∴EF=EH,
在Rt△DEH中,∵∠EDH=30°,
∴DE=2EFH,
∴DE=2EF.
(3)解:结论:BE2=EDEC.
理由:如图3中,
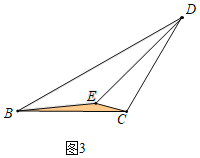
∵∠BED=150°,∠DEC=60°,
∴∠BEC=360°∠BED﹣∠DEC=360°﹣150°﹣60°=150°,
∴∠BED=∠BEC,
∴∠EBD+∠EDB=30°,
∵∠EBD+∠EBC=30°,
∴∠BDE=∠EBC,
∴△DEB∽△BEC,
∴![]() ,
,
∴BE2=DEEC.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
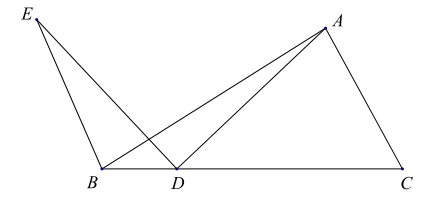
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.△ABC的顶点在格点上,A(1,0)、C(0,7).
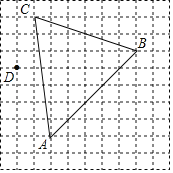
(1)在方格纸中画出平面直角坐标系,写出B点的坐标:B ;
(2)直接写出△ABC的形状: ,直接写出△ABC的面积 ;
(3)若D(﹣1,4),连接BD交AC于E,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
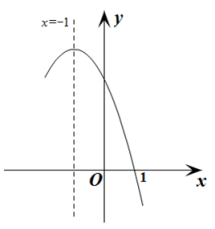
A.①③B.②④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向左平移3个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向左平移3个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含m的式子表示);
(2)求抛物线的对称轴;
(3)已知点P(-1,-m),Q(-3,1).若抛物线与线段PQ恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七巧板是我国古老的益智玩具,受到全世界人的追捧.下图是由一副“现代智力七巧板经无缝拼接且没有重叠的轴对称花朵型图案,直线AB为对称轴,其中①②③是直径为1的圆与半圆,④为直角梯形,⑤为等腰直角三角形,⑥⑦是有一组对边平行且锐角皆为45°的拼板.若已知④的周长是AB的3倍,⑥的周长是AB的5倍,则图中线段AC的长度为_____.
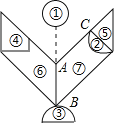
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿CB向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com