
 -2,
-2, .
. AC=1.
AC=1.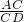 =
= ,
,
 =
= ,
, ,DH=2+
,DH=2+ ,
, )2+(2+
)2+(2+ )2=2AE′,
)2=2AE′, .
.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
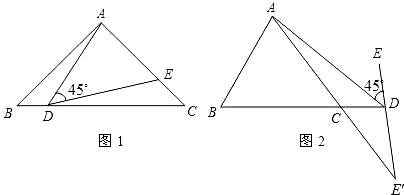
 25、一般来说,依据数学研究对象本质属性的相同点和差异点,将数学对象分为不同种类的数学思想叫做“分类”的思想;将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法.请依据分类的思想和分类讨论的方法解决下列问题:
25、一般来说,依据数学研究对象本质属性的相同点和差异点,将数学对象分为不同种类的数学思想叫做“分类”的思想;将事物进行分类,然后对划分的每一类分别进行研究和求解的方法叫做“分类讨论”的方法.请依据分类的思想和分类讨论的方法解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
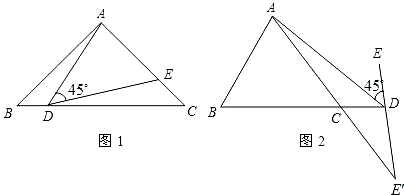
查看答案和解析>>
科目:初中数学 来源:第29章《相似形》中考题集(07):29.4 三角形相似的条件(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《图形的相似》(06)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年广东省佛山市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com