
����Ŀ����ֱ֪��y=kx+3��1-k��������kΪ������k��0����kȡ��ͬ��ֵʱ���ɵò�ֱͬ�ߣ���̽����Щֱ�ߵĹ�ͬ������
ʵ������
��1����k=1ʱ��ֱ��l1�Ľ���ʽΪ ������ͼ1�л���ͼ��k=2ʱ��ֱ��l2�Ľ���ʽΪ ������ͼ2�л���ͼ��
̽������
��2��ֱ��y=kx+3��1-k���ؾ����㣨 �� ����
���Ǩ��
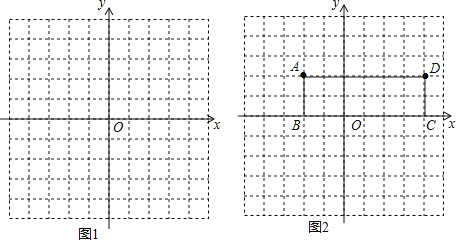
��3������ABCD��ͼ2��ʾ����ֱ��y=kx+k-2��k��0���־���ABCD�����Ϊ��ȵ������֣�����ͼ��ֱ�ӻ�������ֱ�ߣ�
���𰸡���1��y=x����������y=2x-3������������2����3��3������3��������.
��������
��1���ѵ�k=1��k=2ʱ���ֱ������һ�κ����Ľ���ʽ���ɣ�
��2������k��x-3��=y-3���ɵ�����kȡ��ֵ��0���⣩��ֱ��y=kx+3��1-k���ؾ����㣨3��3����
��3�������ֱ��y=kx+k-2��k��0������kȡ��ֵ���ܹ��㣨-1��-2������ȷ�����ζԽ��ߵĽ��㼴�ɻ���ֱ�ߣ�
��1����k=1ʱ��ֱ��l1�Ľ���ʽΪ��y=x��
��k=2ʱ��ֱ��l2�Ľ���ʽΪy=2x-3��
��ͼ1��

��2����y=kx+3��1-k����
��k��x-3��=y-3��
������kȡ��ֵ��0���⣩��ֱ��y=kx+3��1-k���ؾ����㣨3��3����
��3����ͼ2��
��ֱ��y=kx+k-2��k��0��
��k��x+1��=y+2��
�ࣨk��0������kȡ��ֵ���ܹ��㣨-1��-2����
�ҳ��Խ��ߵĽ��㣨1��1����ͨ�������ֱ��ƽ�־���ABCD�������


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߣ�y=ax2+bx+c��a��0������A��2��4����B����1��1�����㣬��������Ϊ��h��k������������ȷ���۵�����ǣ�������
��b��1����c��2����h��![]() ����k��1��
����k��1��
A. �٢ڢۢ� B. �٢ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݽ�������գ�д���������ɻ���ݣ���
��ͼ����֪��DAF=��F����B=��D����˵��AB//DC

֤���ߡ�DAF=��F�� ��֪��
��AD��BF ( )
���D=��DCF( )
�ߡ�B=��D( )
��� =��DCF������������
��AB//DC( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ţ��ij��O��ʼ�ض�������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ���������еĸ���·������Ϊ����λ�����ף���![]() .�ʣ�
.�ʣ�
��1����ţ����Ƿ�ص�������O��
��2����ţ�뿪������O��Զ�Ƕ������ף�
��3�������й����У����ÿ����1������һ��֥�飬����ţ�ɵõ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1��CΪ�߶� AB��һ�㣬�� AC��BCΪһ�ߣ��� ABͬ���������� ACDE�ͳ����� CBFG���� ���� AC=2AE��CB=2BF���� AC2a��BC2b(a b) .
��1���dz����� ACDE�����Ϊ s1 �������� CBFG�����Ϊ s2 .�� AB6, a2b ���� s1 s2 .
��2����ͼ 2���� P���߶� CA�ϵĶ���.
�ٵ��� P�ӵ� C�����ƶ�![]() ����λ������EAP����FBP�����֮��.
����λ������EAP����FBP�����֮��.
�ڵ��� P�ӵ� C�����ƶ� ![]() ����λ����EAP����FBP�����֮���Ϊ m1 �� ���� P�ӵ� C�����ƶ� (a b) ����λ����EAP����FBP�����֮���Ϊ m2 ����
����λ����EAP����FBP�����֮���Ϊ m1 �� ���� P�ӵ� C�����ƶ� (a b) ����λ����EAP����FBP�����֮���Ϊ m2 ���� ![]() ��ֵ������ú� n �Ĵ���ʽ��ʾ��.
��ֵ������ú� n �Ĵ���ʽ��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���쳵������ͬʱ�Ӽس�����������ʻ���쳵�����ҵغ�ԭ·���ؼأ����������ҵ�ֹͣ��ͼ�ٱ�ʾ������ʻ��������ص�·��y��km�������ʱ��x��h���ĺ���ͼ������ͼ���е���Ϣ������������⣺
��1���쳵���ٶ�Ϊ km/h���������ٶ�Ϊ�� ��km/h���������صľ���Ϊ�� ��km��
��2��������ʱ�䣬�������100km��
��3��������֮��ľ���Ϊs km����ͼ�ڵ�ֱ������ϵ�л���s��km����x��h���ĺ���ͼ��
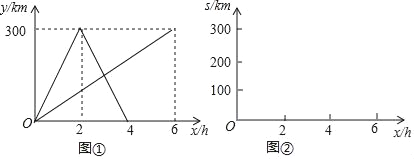
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���![]() ��
��
��1����֤����������ʵ��m������������������ȵ�ʵ������
��2�������̵�һ������1����m��ֵ�����̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A1B1C1O��A2B2C2C1��A3B3C3C2��������ͼ�ķ�ʽ���ã���A1��A2��A3�����͵�C1��C2��C3�����ֱ���ֱ��y=x+1��x���ϣ����B6��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
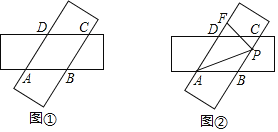
����Ŀ�����ſ��Ⱦ�Ϊ4�ľ���ֽƬ����ͼ��ʾ��ʽ���ã�
��1����ͼ1����֤���ı���ABCD�����Σ�
��2����ͼ2����P��BC�ϣ�PF![]() AD�ڵ�F����
AD�ڵ�F����![]() =16
=16![]() , PC=1.
, PC=1.
�����BAD�Ķ���������DF�ij�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com