
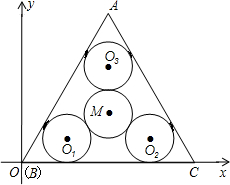
 的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
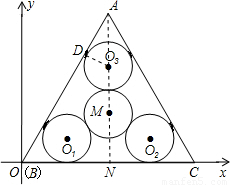 解:(1)连接AM并延长交BC于N,
解:(1)连接AM并延长交BC于N, ∠BAC=30°,
∠BAC=30°,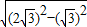 =3,
=3,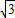 ,1),
,1),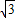 ,1).
,1).

科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在上劳技课时,张老师拿出一张边长为![]() 的等边
的等边![]() 纸片,现要在这块纸片上裁剪出四个圆,若记这块
纸片,现要在这块纸片上裁剪出四个圆,若记这块![]() 纸片的中心为
纸片的中心为![]() ,半径为
,半径为![]() ,在
,在![]() 内部画一个⊙M后,再作三个半径都为
内部画一个⊙M后,再作三个半径都为![]() 的等圆⊙
的等圆⊙![]() 、⊙
、⊙![]() 、⊙
、⊙![]() ,使它们分别与
,使它们分别与![]() 的两边相切,与⊙M外切,建立直角坐标系如图所示.
的两边相切,与⊙M外切,建立直角坐标系如图所示.
(1)写出点M的坐标;
(2)求出![]() 与
与![]() 的函数关系式,并求自变量
的函数关系式,并求自变量![]() 的取值范围约在哪两个数之间(精确到0.1);
的取值范围约在哪两个数之间(精确到0.1);
(3)若记这四个圆的面积总和为![]() , 试问
, 试问![]() 有最小值吗?若有,求出这个最小值,并写出相应的
有最小值吗?若有,求出这个最小值,并写出相应的![]() 值.
值.

查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考数学模拟试卷(一)(解析版) 题型:解答题
 的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com