
| A. | (a-10%)(a+15%)万元 | B. | a(1-90%)(1+85%)万元 | C. | a(1-10%)(1+15%)万元 | D. | a(1-10%+15%)万元 |
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
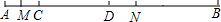 如图,已知线段AB=14,在AB上有C,D,M,N四点,且满足AC:CD:DB=1:2:4,AC=2AM,DB=4DN.求:MN的长度.
如图,已知线段AB=14,在AB上有C,D,M,N四点,且满足AC:CD:DB=1:2:4,AC=2AM,DB=4DN.求:MN的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
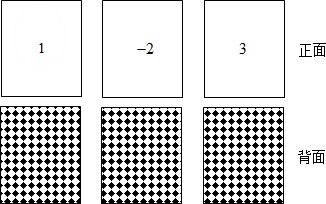
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
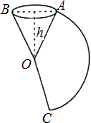 如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
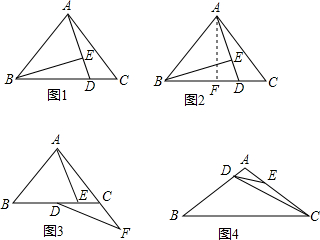
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com