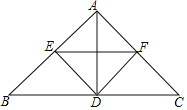
【题目】如图，在△ABC中，AB=AC，D是边BC上的一点，DE⊥AB，DF⊥AC，垂足分别是E、F，EF∥BC．
（1）求证：△BDE≌△CDF；
（2）若BC=2AD，求证：四边形AEDF是正方形．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：
（1）用ASA证明△BDE≌△CDF；
（2）由BC=2AD，得∠BAC=90°，从而四边形AEDF是矩形，再由AE=AF即可得证.
试题解析：
证明：（1）∵AB=AC，∴∠B=∠C，
∵EF∥BC，∴∠AEF=∠B，∠AFE=∠C，∴∠AEF=∠AFE，
∴AE=AF，∴BE=CF，
∵DE⊥AB，DF⊥AC，∴∠AED=∠AFD=90°，
在△BED和△CFD中，
，
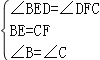∴△BDE≌△CDF．
（2）∵△BDE≌△CDF，∴BD=DC，DE=DF，
∵BC=2AD，∴AD=
BC，∴∠BAC=90°，
∵DE⊥AB，DF⊥AC，∴∠EAF=∠AED=∠AFD=90°，∴四边形AEDF是矩形，
∵AE=AF，∴四边形AEDF是正方形．
仁爱英语同步练习册系列答案
学习实践园地系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，O为坐标原点，点M、N位于第一象限，其中M的坐标为（m，5），点N的坐标（n，8），且m≥n．
（1）若MN与坐标轴平行，则MN＝ ；
（2）若m、n、t满足
，MA⊥x轴，垂足为A，NB⊥x轴，垂足为B．
①求四边形MABN的面积；
②连接MN、OM、ON，若△MON的面积大于26而小于30，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，在AD上截取AE=AB，连接BE，EO，并求∠BEO的角度（要求：尺规作图，保留痕迹，不写作法）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．
（1）求证：AE=CF；
（2）若AB=6，∠COD=60°，求矩形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，△ABC（如图）．
（1）利用尺规按下列要求作图（保留作图痕迹，不写作法）：
①作∠BAC的平分线AD，交BC于点D；
②作AB边的垂直平分线EF，分别交AD，AB于点E，F．
（2）连接BE，若∠ABC＝60°，∠C＝40°，求∠AEB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF．
（1）求证：四边形ADCF是平行四边形；
（2）当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
：
与
轴交于点
，直线
：
与轴交于点
，且经过点
，直线，交于点
．
（1）求
的值；
（2）求直线的解析式；
（3）根据图象，直接写出
的解集．
（4）求
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角板ABC和三角板BDE（∠ACB=∠DBE=90°，∠ABC=60°）按不同的位置摆放.
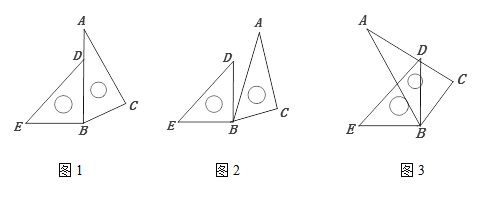
（1）如图1，若边BD，BA在同一直线上，则∠EBC= ；
（2）如图2，若∠EBC=165°，那么∠ABD= ；
（3）如图3，若∠EBC=120°，求∠ABD的度数。
查看答案和解析>>
科目：初中数学 来源： 题型：
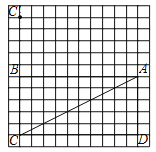
【题目】如图，12×12的正方形网格中的每个小正方形的边长都是1，正方形的顶点叫做格点．矩形ABCD的四个顶点A，B，C，D都在格点上，将△ADC绕点A顺时针方向旋转得到△AD′C′，点C与点C′为对应点．
（1）在正方形网格中确定D′的位置，并画出△AD′C′；
（2）若边AB交边C′D′于点E，求AE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com