练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如果（x+1）6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6，试求：a1+a3+a5．

    分析 根据二项展开式的通项公式展开可得a1+a3+a5．=C${\;}_{6}^{1}$+C${\;}_{6}^{3}$+C${\;}_{6}^{5}$，计算求出结果．

    解答 解：a1+a3+a5．=C${\;}_{6}^{1}$+C${\;}_{6}^{3}$+C${\;}_{6}^{5}$=32．

    点评 本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式某项的系数，属于中档题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．已知一次函数y=$\frac{3}{2}$x+a与y=-$\frac{1}{2}$x+b的图象都经过点A（-2，0），且与y轴分别交于B，C两点，那么△ABC的面积是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．计算：（-3）+5的结果是（　　）
    A．-2B．2C．8D．-8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

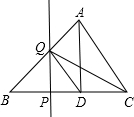    7．如图，△ABC中，AD⊥BC，垂足为D，AD=BD=3，CD=2，点P从点B出发沿线段BC的方向移动到点C停止，过点P作PQ⊥BC，交折线BA-AC于点Q，连接DQ、CQ，若△ADQ与△CDQ的面积相等，则线段BP的长度是（　　）
    A．$\frac{9}{5}$或4B．$\frac{6}{5}$或4C．$\frac{9}{5}$或$\frac{13}{5}$D．$\frac{6}{5}$或$\frac{13}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

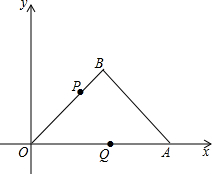    14．如图，∠OAB=45°，点A的坐标是（4，0），AB=$2\sqrt{2}$，连结OB．
    （1）直接写出点B的坐标．
    （2）动点P从点O出发，沿折线O-B-A方向向终点A匀速运动，另一动点Q从点O出发，沿OA方向匀速运动，若点P的运动速度为$\sqrt{2}$个单位/秒，点Q的运动速度是1个单位/秒，P、Q两点同时出发，设运动时间为t秒，请求出使△OPQ的面积等于1.5时t的值．
    （3）动点P仍按（2）中的方向和速度运动，但Q点从A点向O点运动，速度为1个单位/秒，P、Q与△OAB中的任意一个顶点形成直角三角形时，求此时t（t≠0）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A，D分别落在A′，D′处，且A′D′经过点B，EF为折痕，当D′F⊥CD时，$\frac{CF}{BE}$的值为（　　）
    A．$\frac{3-\sqrt{3}}{2}$B．$\frac{3+\sqrt{3}}{2}$C．$\frac{3-\sqrt{3}}{3}$D．$\frac{3+\sqrt{3}}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．用适当的方法解方程：
    （1）x2-4x+3=0；                
    （2）（x-2）（3x-5）=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

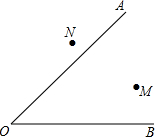    8．已知∠AOB，点M、N，在∠AOB的内部求作一点P．使点P到∠AOB的两边距离相等，且PM=PN（要求：尺规作图，保留作图痕迹，不写作法）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．金秋十月，又到了食蟹的好季节啦！某经销商去水产批发市场采购太湖蟹，他看中了A、B两家的某种品质相近的太湖蟹．零售价都为60元/千克，批发价各不相同．
    A家规定：批发数量不超过100千克，按零售价的92%优惠；批发数量超过100千克但不超过200千克，按零售价的90%优惠；超过200千克的按零售价的88%优惠．
    B家的规定如表：
    数量范围
    （千克）    		0～50部分
    （含50）    		50以上～150部分（含150，不含50）150以上～250部分（含250，不含150）250以上部分
    （不含250）
    价格（元）零售价的95%零售价的85%零售价的75%零售价的70%
    （1）如果他批发80千克太湖蟹，则他在A 家批发需要4416元，在B家批发需要4380元；
    （2）如果他批发x千克太湖蟹 （150＜x＜200），则他在A 家批发需要54x元，在B家批发需要45x+1200元（用含x的代数式表示）；
    （3）现在他要批发180千克太湖蟹，你能帮助他选择在哪家批发更优惠吗？请说明理由．

    查看答案和解析>>

    同步练习册答案