
【题目】(1)如图1,正方形ABCD中,E、F分别是AD、DC边上的点,CE与BF交于点G,BF⊥CE,求证:BF=CE;
(2)如图2,矩形ABCD中,AB=2AD,E、F分别是AD、DC边上的点,CE与BF交于点G,∠A+∠BGE=180°,求证:CE=2BF;
(3)如图3,若(2)中的四边形ABCD是平行四边形,且∠A<90°,则CE=2BF是否仍然成立?若成立,请证明;若不成立,请说明理由.
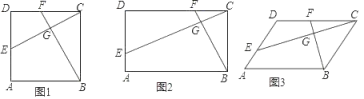
【答案】(1)见解析;(2)见解析;(3)成立,证明见解析.
【解析】
(1)只要证明△CDE≌△BCF,即可解决问题;
(2)先根据∠CFG+∠DCE=90°,∠CED+∠DCE=90°,判断出∠CFB=∠DEC,进而得出△CDE∽△BCF,即可得出结论;
(3)先判断出∠BFC=∠BCG,进而得出△BCG∽△BFC,即![]() ,再判断出△CFG∽△CED,得出
,再判断出△CFG∽△CED,得出![]() ,即可得出结论;
,即可得出结论;
(1)如图1中,
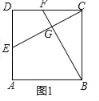
∵四边形ABCD是正方形,
∴CD=BC,∠D=∠BCF=90°,
∵BF⊥CE,
∴∠BGC=90°,
∴∠CBF+∠BCG=90°,∠BCG+∠DCE=90°,
∴∠DCE=∠CBF,
∴△CDE≌△BCF,
∴BF=CE
(2)如图2中,
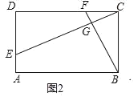
∵四边形ABCD是矩形,
∴CD=AB,BC=AD,∠A=∠D=∠BCD=90°,
∵AB=2AD,
∴CD=2BC,
∵∠A+∠BGE=180°,
∴∠CGF=∠BGE=90°=∠D,
∴∠CFG+∠DCE=90°,
∵∠CED+∠DCE=90°,
∴∠CFB=∠DEC,
∵∠D=∠BCF,
∴△CDE∽△BCF,
∴![]() =2,
=2,
∴CE=2BF;
(3)如图3中,
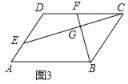
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,CD=AB,BC=AD,
∵AB=2AD,
∴CD=2BC,
∵∠A+∠BGE=180°,∠BGE+∠BGC=180°,
∴∠BGC=∠A=∠BCD,
∵∠BGC=∠BFC+∠FCG,∠BCD=∠BCG+∠FCG,
∴∠BFC=∠BCG,
∵∠CBF=∠FBC,
∴△BCG∽△BFC,
∴![]() ,
,
∵∠A+∠D=180°,∠A+∠CGF=180°,
∴∠D=∠CGF,
∵∠FCG=∠ECD,
∴△CFG∽△CED,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵CD=2BC,
∴CE=2BF.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】万美服装店准备购进一批两种不同型号的衣服,已知若购进A型号的衣服9件,B型号的衣服10件共需1 810元;若购进A型号的衣服12件,B型号的衣服8件共需1 880元.已知销售一件A型号的衣服可获利18元,销售一件B型号的衣服可获利30元.
(1)求A、B型号衣服的进价各是多少元?
(2)若已知购进的A型号的衣服比B型号衣服的2倍还多4件,且购进的A型号的衣服不多于28件,则该服装店要想获得的利润不少于699元,在这次进货时可有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生200米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
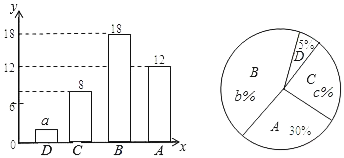
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
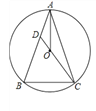
【题目】如图,△ABC内接于⊙O,AB=AC,CO的延长线交AB于点D.
(1)求证:AO平分∠BAC;
(2)若BC=6,sin∠BAC=![]() ,求AC和CD的长.
,求AC和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=-4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=-4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.

(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
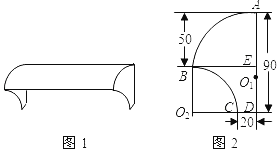
【题目】小帅家的新房子刚装修完,便遇到罕见的大雨,于是他向爸爸提议给窗户安上遮雨罩.如图1所示的是他了解的一款雨罩.它的侧面如图2所示,其中顶部圆弧AB的圆心O在整直边缘D上,另一条圆弧BC的圆心O.在水平边缘DC的廷长线上,其圆心角为90°,BE⊥AD于点E,则根据所标示的尺寸(单位:c)可求出弧AB所在圆的半径AO的长度为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居城市,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
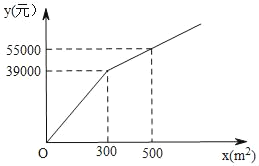
(1)试求出y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉的种植面积的2倍.
①试求种植总费用W元与种植面积x(m2)之间的函数关系式;
②应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用W最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com