
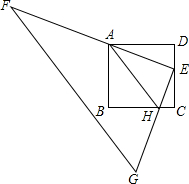
 如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;
如图,正方形ABCD的边长为4,Rt△FEG的直角顶点E在正方形的边DC上运动,一条直角边EF始终经过点A,另一直角边EG交正方形的边BC于点H;分析 (1)首先根据已知条件证得△ADE∽△ECH,得到$\frac{AD}{CE}$=$\frac{AE}{EH}$,由于DE=CE,推出$\frac{AD}{DE}$=$\frac{AE}{EH}$,得出△ADE∽△AEH;
(2)设DE=x,四边形AHCD的面积为S,则CE=4-x,根据梯形的面积公式列出函数关系式,根据二次函数的顶点坐标公式得出结果.
解答 解:(1)∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∵∠FEG=90°,
∴∠AED+∠DAE=∠AED+∠CEH=90°,
∴∠DAE=∠CEH=90°,
∴△ADE∽△ECH,
∴$\frac{AD}{CE}$=$\frac{AE}{EH}$,
∵DE=CE,
∴$\frac{AD}{DE}$=$\frac{AE}{EH}$,
∵∠D=∠AEH,
∴△ADE∽△AEH;
(2)设DE=x,四边形AHCD的面积为S,则CE=4-x,
∵△ADE∽△ECH,
∴$\frac{AD}{CE}$=$\frac{DE}{CH}$,
∴$\frac{4}{4-x}$=$\frac{x}{CH}$,
∴CH=$\frac{{-x}^{2}+4x}{4}$,
∴S=$\frac{1}{2}$($\frac{{-x}^{2}+4x}{4}$+4)×4=-$\frac{1}{2}$(x-2)2+10,
∴当x=2时,S最大值=10,
∴当DE=2时,四边形AHCD的面积最大,最大值是10.
点评 本题考查了正方形的性质,相似三角形的判定和性质,梯形的面积公式,关键是找准三角形相似的条件.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
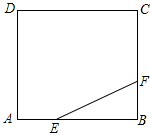 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
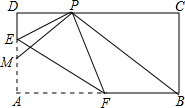 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
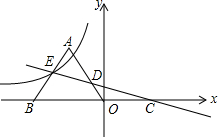 如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )
如图,△OAB为等腰直角三角形,斜边OB边在x负半轴上,一次函数y=-$\frac{1}{7}$x+$\frac{4}{7}$与△OAB交于E、D两点,与x轴交于C点,反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支过E点,若S△AED=S△DOC,则k的值为( )| A. | -$\frac{6}{7}$ | B. | -$\sqrt{3}$ | C. | -3 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
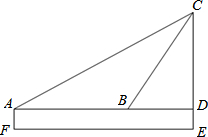 九年级五班某同学为了测量某市电视台的高度,进行了如下操作:
九年级五班某同学为了测量某市电视台的高度,进行了如下操作:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 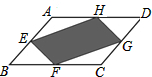 | B. | 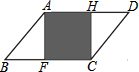 | ||
| C. | 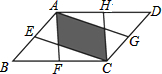 | D. | 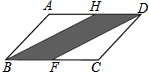 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com