
分析 根据分式的加减法和除法可以化简题目中的式子,然后对x2+4x-3=0变形即可解答本题.
解答 解:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}÷(\frac{12}{x+2}-x+2)+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}÷\frac{12-(x-2)(x+2)}{x+2}+\frac{1}{x+4}$
=$\frac{(x-4)^{2}}{x(x+2)}•\frac{x+2}{-(x+4)(x-4)}+\frac{1}{x+4}$
=$\frac{4-x}{x(x+4)}+\frac{1}{x+4}$
=$\frac{4-x+x}{x(x+4)}$
=$\frac{4}{{x}^{2}+4x}$,
∵x2+4x-3=0,
∴x2+4x=3,
∴原式=$\frac{4}{3}$.
点评 本题考查分式的化简求值、一元二次方程的解,解答本题的关键是明确分式化简求值的方法.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.
如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN,AC=6,BD=8,求AM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
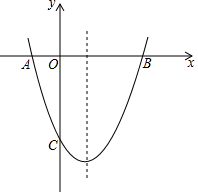 抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,点B的坐标为(3,0),点C的坐标为(0,-3)
抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线的对称轴为x=1,点B的坐标为(3,0),点C的坐标为(0,-3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
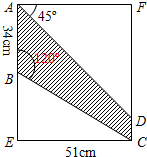 在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).
在2016首届合肥风筝文化节期间,某校丁周同学想在一个矩形材料中剪出如图阴影所示的图形,作为要制作的风筝的一个翅膀,请你根据图中的数据帮丁周同学计算出BE、CD的长度(精确到个位,$\sqrt{3}$≈1.7).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com