
【题目】已知下面四个图形中,AB∥CD,探究四个图形中,∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC与∠PAB,∠PCD的关系是__________________;
(2)图②中,∠APC与∠PAB,∠PCD的关系是__________________;
(3)请你在图③和图④中任选一个,说明∠APC与∠PAB,∠PCD的关系,并加以证明



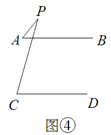
【答案】 ∠APC = ∠PAB+∠PCD; ∠APC +∠PAB+∠PCD = 360°
【解析】分析:(1)、过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,内错角相等可得∠PAB=∠APE,∠PCD=∠CPE,然后根据∠APC=∠APE+∠CPE整理即可;(2)、过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠APE+∠CPE整理即可;(3)、图(3)过点P作PM∥AB,根据平行公理可得AB∥PM∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APM=180°,∠PCD+∠CPM=180°,然根据∠APC=∠CPM-∠APM整理即可.
详解:(1)∠APC = ∠PAB+∠PCD; (2)∠APC +∠PAB+∠PCD = 360°;
(3)如图∠PAB =∠PCD+∠APC ,
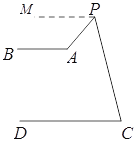
理由是:过点P作PM∥AB, ∵PM∥AB, ∴AB∥CD , ∴PM∥CD,
∴∠BAP+∠MPA= 180°,∠PCD+∠APC+∠MPA= 180°, ∴∠BAP = ∠PCD+∠APC.


科目:初中数学 来源: 题型:
【题目】小强、小亮、小文三位同学玩投硬币游戏.三人同时各投出一枚均匀硬币,若出现三个正面向上或三个反面向上,则小强赢;若出现2个正面向上一个反面向上,则小亮赢;若出现一个正面向上2个反面向上,则小文赢.下面说法正确的是( )
A.三人赢的概率都相等
B.小文赢的概率最小
C.小亮赢的概率最小
D.小强赢的概率最小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,二次函数图像的顶点为A(1,﹣4),且过点B(3,0). 
(1)求该二次函数的解析式;
(2)将该二次函数图像向右平移几个单位,可使平移后所得图像经过坐标原点?并直接写出平移后所得图像与x轴的另一个交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com