
 £¬OB=4£¬ĻÖ½«Rt”÷AOBČĘ×ÅÖ±½Ē¶„µćO°“ÄꏱÕė·½ĻņŠż×Ŗ90”ćµĆµ½”÷COD£¬ŅŃÖŖŅ»Å×ĪļĻß¾¹żC”¢D”¢BČżµć£®
£¬OB=4£¬ĻÖ½«Rt”÷AOBČĘ×ÅÖ±½Ē¶„µćO°“ÄꏱÕė·½ĻņŠż×Ŗ90”ćµĆµ½”÷COD£¬ŅŃÖŖŅ»Å×ĪļĻß¾¹żC”¢D”¢BČżµć£®
|
|
| 1 |
| 2 |
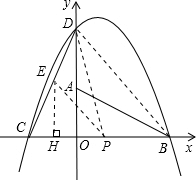 £Ø2£©¹żE×÷EH”ĶxÖį£¬
£Ø2£©¹żE×÷EH”ĶxÖį£¬| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| EH |
| OD |
| CP |
| BC |
| EH |
| 4 |
| m+2 |
| 6 |
| 2m+4 |
| 3 |
| 1 |
| 2 |
| 2m+4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 15 |
| 15 |
| 15 |
| 15 |



 ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø
ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø ½šÅĘ½ĢøØÅąÓÅÓÅŃ”¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
½šÅĘ½ĢøØÅąÓÅÓÅŃ”¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
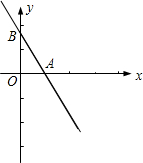 ÓŚµćB£¬tan”ĻOAB=
ÓŚµćB£¬tan”ĻOAB=| 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
 60”ć£®·É»ś¼ĢŠų·ÉŠŠ0.1Ē§Ć×µ½“ļE“¦½ųŠŠæÕĶ¶£¬ŅŃÖŖæÕĶ¶Īļ׏ŌŚæÕÖŠĻĀĀä¹ż³ĢÖŠµÄ¹ģ¼£ŹĒÅ×ĪļĻߣ¬ČōŅŖŹ¹æÕĶ¶Īļ׏øÕŗĆĀäŌŚO“¦£®
60”ć£®·É»ś¼ĢŠų·ÉŠŠ0.1Ē§Ć×µ½“ļE“¦½ųŠŠæÕĶ¶£¬ŅŃÖŖæÕĶ¶Īļ׏ŌŚæÕÖŠĻĀĀä¹ż³ĢÖŠµÄ¹ģ¼£ŹĒÅ×ĪļĻߣ¬ČōŅŖŹ¹æÕĶ¶Īļ׏øÕŗĆĀäŌŚO“¦£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā
| x | ” | -1 | 0 | 1 | 2 | ” |
| y | ” | 10 | 5 | 2 | 1 | ” |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ²»Ļź ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com