
【题目】一列火车匀速行驶,经过一条长300米的隧道需要20秒的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒.求这列火车的长度.
小冉根据学习解决应用问题的经验对上面问题进行了探究,下面是小冉的探究过程,请补充完成:
设这列火车的长度是x米,那么
(1)从车头经过灯下到车尾经过灯下,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(2)从车头进入隧道到车尾离开隧道,火车所走的路程是 米,这段时间内火车的平均速度是 米/秒;
(3)火车经过灯下和火车通过隧道的平均速度的关系是 ;
(4)由此可以列出方程并求解出这列火车的长度(请列方程求解)
【答案】(1)x,![]() ;(2)(x+300);
;(2)(x+300);![]() ;(3)相等;(4)这列火车的长度300m.
;(3)相等;(4)这列火车的长度300m.
【解析】
(1)根据火车长度为xm,根据题意列出代数式即可;
(2)根据题意列出代数式即可;
(3)上述问题中火车的平均速度不发生变化;
(4)根据速度相等列出方程,求出方程的解即可得到结果.
(1)根据题意得:从车头经过灯下到车尾经过灯下火车所走的路程为xm,
这段时间内火车的平均速度![]() m/s.
m/s.
故答案为:x, ![]() ;
;
(2)从车头进入隧道到车尾离开隧道火车所走的路程为(x+300)m,
这段时间内火车的平均速度为![]() m/s.
m/s.
故答案为:(x+300); ![]() ;
;
(3)速度没有发生变化,即火车经过灯下和火车通过隧道的平均速度的关系是相等。
故答案为:相等;
(4)根据题意得:![]() ,
,
解得:x=300.
答:这列火车的长度300m.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】阅读材料.
某校七年级共有10个班,320名同学,地理老师为了了解全年级同学明年选考时,选修地理学科的意向,请小丽,小明,小东三位同学分别进行抽样调查.三位同学调查结果反馈如图:

(1)小丽、小明和小东三人中,你认为哪位同学的调查结果较好地反映了该校七年级同学选修地理的意向,请说出理由.
(2)估计全年级有意向选修地理的同学的人数为 人,理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八达岭森林体验中心,由八达岭森林体验馆和450公顷的户外体验区构成。森林体验馆包括"八达岭森林变迁"、"八达岭森林大家族"、"森林让生活更美好"等展厅,户外游憩体验系统根据森林生态旅游最新理念,采取少设施、设施集中的点线布局模式,突破传统的"看风景"旅游模式,强调全面体验森林之美。
在室内展厅内,有这样一个可以动手操作体验的仪器,如图小明在社会大课堂活动中,记录了这样一组数字:

交通 工具 | 行驶100公里的碳足迹(Kg) | 100公里碳中 和树木棵树 |
飞机 | 13.9 | 0.06 |
小轿车 | 22.5 | 0.10 |
公共汽车 | 1.3 | 0.005 |
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地。
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )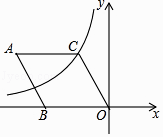
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
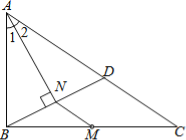
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形中ABCD,点E为AB边上的一点,点F为对角线BD上的一点,且EF⊥AB.
(1)若四边形ABCD为正方形.
①如图1,请直接写出AE与DF的数量关系;
②将△EBF绕点B逆时针旋转到图2所示的位置,连接AE,DF,猜想AE与DF的数量关系并说明理由;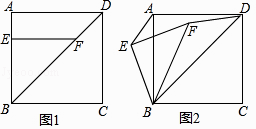
(2)如图3,若四边形ABCD为矩形,BC=mAB,其它条件都不变,将△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',连接AE',DF',请在图3中画出草图,并直接写出AE'与DF'的数量关系.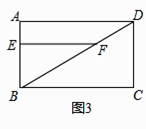
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com