
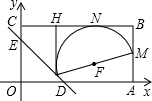
 如图,在平面直角坐标中,矩形OABC,OA=4,AB=2,直线
如图,在平面直角坐标中,矩形OABC,OA=4,AB=2,直线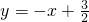 与坐标轴交于D,E两点,设M是AB的中点,P是线段DE上的动点.过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,梯形PMBH的面积是________.
与坐标轴交于D,E两点,设M是AB的中点,P是线段DE上的动点.过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,梯形PMBH的面积是________. +
+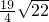
 上,所以P(x,-x+
上,所以P(x,-x+ ),根据题意可得PN⊥MN,FN⊥BC,F是圆心,又因N是线段HB的中点,HN=NB=
),根据题意可得PN⊥MN,FN⊥BC,F是圆心,又因N是线段HB的中点,HN=NB=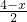 ,PH=2-(-x+
,PH=2-(-x+ )=x+
)=x+ ,BM=1,利用直径对的圆周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°,所以∠HPN=∠BNM,又因∠PHN=∠B=90°,所以可得到Rt△PNH∽Rt△NMB,所以
,BM=1,利用直径对的圆周角是直角可得到∠HPN+∠HNP=∠HNP+∠BNM=90°,所以∠HPN=∠BNM,又因∠PHN=∠B=90°,所以可得到Rt△PNH∽Rt△NMB,所以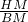 =
=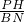 ,∴
,∴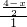 =
=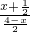 ,这样就可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以SPMBH=
,这样就可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以SPMBH=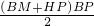 =
=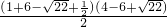 =-
=- +
+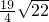 .
.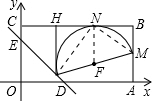 解:设P(x,y),连接PN、MN、NF,
解:设P(x,y),连接PN、MN、NF, 上,
上, ),
),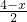 ,PH=2-(-x+
,PH=2-(-x+ )=x+
)=x+ ,BM=1,
,BM=1,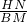 =
=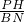 ,
,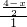 =
=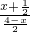 ,
, (x>
(x> 舍去),x=6-
舍去),x=6- ,
,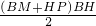 =
=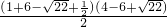 =-
=- +
+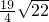 .
. +
+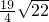 .
.

科目:初中数学 来源: 题型:
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com