
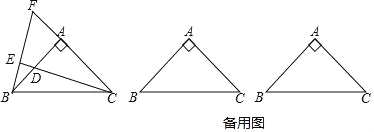
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,请证明:BD=AB﹣AF;
(2)试探索:点D在AB的延长线或反向延长线上时,请在备用图中画出图形,(1)中的结论是否成立?若不成立,请直接写出正确结论(不需要证明).
【答案】(1)证明见解析(2)结论不成立
【解析】
(1)易证∠FBA=∠FCE,结合条件容易证到△FAB≌△DAC,从而有FA=DA,就可得到AB=AD+BD=FA+BD.
(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.
(1)证明∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°,
∴∠FBA=∠FCE,
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC,
在△FAB和△DAC中, ,
,
∴△FAB≌△DAC(ASA),
∴FA=DA,
∴AB=AD+BD=FA+BD,
∴BD=AB-AF;
(2)解:(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
①当点D在AB的延长线上时,如图2.

同理可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.

同理可得:FA=DA.
则AB=BD-AD=BD-AF.


科目:初中数学 来源: 题型:
【题目】张明和李强两名运动爱好者周末相约到东湖绿道进行跑步锻炼.(1)周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的绿道落雁岛入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,求张明和李强的速度分别是多少米/分?
(1)两人到达绿道后约定先跑 6 千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=12,n=5时,求李强跑了多少分钟?
②张明的跑步速度为 米/分(直接用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿色出行,低碳健身”已成为广大市民的共识.为方便市民出行,东台市推出了公共自行车系统,收费以小时为单位,每次使用不超过1小时的免费,超过1小时后,不足1小时的部分按1小时收费.小红同学通过调查得知,自行车使用时间为3小时,收费2元;使用时间为4小时,收费3元.她发现当使用时间超过1小时后用车费用与使用时间之间存在一次函数的关系.
(1)设使用自行车的费用为![]() 元,使用时间为
元,使用时间为![]() 小时(
小时(![]() 为大于1的整数),求
为大于1的整数),求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若小红此次使用公共自行车5小时,则她应付多少元费用?
(3)若小红此次使用公共自行车付费6元,求她所使用自行车的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
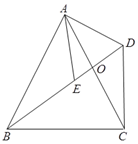
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
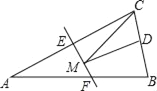
A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
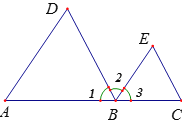
【题目】如图,A、B、C在同一直线上,
(1)若∠A=∠3,依据__________,可得______∥_______;
(2)若∠______=∠______,则依据内错角相等,两直线平行,可得DB∥EC;
(3)若∠______+∠_______=180°,则AD∥BE,依据是____________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com