
【题目】顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
A. 正方形 B. 菱形 C. 矩形 D. 梯形
【答案】C
【解析】根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
如图:
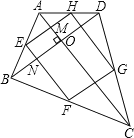
如图,AC⊥BD,E. F. G、H分别为各边的中点,连接点E. F. G、H.
∵E、F. G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD(三角形的中位线平行于第三边),
∴四边形EFGH是平行四边形(两组对边分别平行的四边形是平行四边形),
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故选:B.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点且与反比例函数
的图象与x轴、y轴分别交于A、B两点且与反比例函数![]() 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥![]() 轴于D点,若∠CAD=
轴于D点,若∠CAD=![]() ,AB =
,AB =![]() ,CD =
,CD =![]()
(1)求点A、B、D的坐标;
(2)求一次函数的解析式;
(3)反比例函数的解析式;
(4)求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
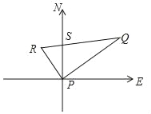
【题目】如图,某港口P位于东西方向的海岸线上,A、B两艘轮船同时从港口P出发,各自沿一固定方向航行,A轮船每小时航行12海里,B轮船每小时航行16海里.它们离开港口一个半小时后分别位于点R、Q处,且相距30海里.已知B轮船沿北偏东60°方向航行.
(1)A轮船沿哪个方向航行?请说明理由;
(2)请求出此时A轮船到海岸线的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形 ABCD 中,点 E 是对角线 BD 上一动点,AE 的延长线交 CD 于点 F,交 BC 的延长线于点 G,M 是 FG 的中点.
(1)求证: ∠DAE=∠DCE;
(2)判断线段 CE 与 CM 的位置关系,并证明你的结论;
(3)当![]() ,并且
,并且![]() 恰好是等腰三角形时,求 DE 的长.
恰好是等腰三角形时,求 DE 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一些相同的房间需要粉刷墙面,一天4名一级技工去粉刷10个房间,结果其中有![]() 墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的
墙面未来得及粉刷;同样时间内7名二级技工粉刷了15个房间之外,还多粉刷了另外的![]() 墙面.每名一级技工比二级技工一天多粉刷
墙面.每名一级技工比二级技工一天多粉刷![]() 墙面.设每个房间需要粉刷的墙面面积为
墙面.设每个房间需要粉刷的墙面面积为![]() 平方米,一级技工每天粉刷y平方米,下列方程正确有( )个
平方米,一级技工每天粉刷y平方米,下列方程正确有( )个
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设实数a,b,c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x-a|+|x+b|+|x-c|的最小值为( )
A. ![]() B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母m,n的代数式是:![]() .
.
(1)化简这个代数式.
(2)小明取m,n互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少?
(3)聪明的小智从化简的代数式中发现,只要字母n取一个固定的数,无论字母m取何数,代数式的值恒为一个不变的数,那么小智所取的字母n的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com