
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=![]() ,BC=
,BC=![]() ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F,下列说法:①在旋转过程中,AF=CE. ②OB=AC,③在旋转过程中,四边形ABEF的面积为
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F,下列说法:①在旋转过程中,AF=CE. ②OB=AC,③在旋转过程中,四边形ABEF的面积为![]() ,④当直线AC绕点O顺时针旋转30°时,连接BF,DE则四边形BEDF是菱形,其中正确的是( )
,④当直线AC绕点O顺时针旋转30°时,连接BF,DE则四边形BEDF是菱形,其中正确的是( )
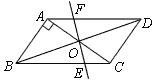
A.①②④B.① ②C.①②③④D.② ③ ④
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() 过点
过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() .设
.设![]()

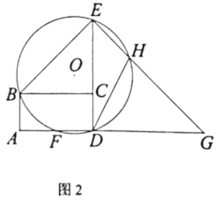
(1)连结![]() ,请求出
,请求出![]() 的度数和
的度数和![]() 的半径(用
的半径(用![]() 的代数式表示). (直接写出答案)
的代数式表示). (直接写出答案)
(2)证明:点![]() 是
是![]() 的中点.
的中点.
(3)如图2,延长![]() 至点
至点![]() ,使得
,使得![]() , 连结
, 连结![]() ,交
,交![]() 于点
于点![]()
①连结![]() ,当
,当![]() 与四边形
与四边形![]() 其它三边中的一边相等时,请求出所有满足条件的
其它三边中的一边相等时,请求出所有满足条件的![]() 的值.
的值.
②当点![]() 关于直线
关于直线![]() 对称点
对称点![]() 恰好落在
恰好落在![]() 上,连结
上,连结![]() .记
.记![]() 和
和![]() 的面积分别为
的面积分别为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形边长都是![]() 个单位长度,
个单位长度,![]() 的顶点均在格点上.建立平面直角坐标系后,点
的顶点均在格点上.建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
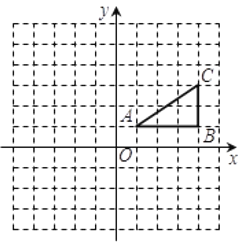
(1)先将![]() 向左平移
向左平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到
个单位长度得到![]() (点
(点![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ),请在图中画出
),请在图中画出![]() ;
;
(2)再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() (点
(点![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ),试在图中画出
),试在图中画出![]() ,并直接写出点
,并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 个单位长度的小正方形组成的
个单位长度的小正方形组成的![]() 的网格中,给出了格点(网格线的交点)为端点的线段
的网格中,给出了格点(网格线的交点)为端点的线段![]()
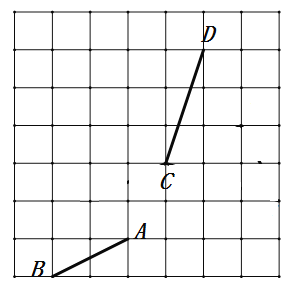
(1)将线段![]() 通过平移使得
通过平移使得![]() 点和
点和![]() 点重合,
点重合,![]() 点的对应点为
点的对应点为![]() ,则应该先将线段
,则应该先将线段![]() 向 平移
向 平移![]() 个单位,再向上平移 个 单位,画出
个单位,再向上平移 个 单位,画出![]() 平移后对应的线段
平移后对应的线段![]() ;
;
(2)将线段![]() 绕
绕![]() 点按顺时针方向旋转
点按顺时针方向旋转![]() 点的对应点为
点的对应点为![]() ,画出线段
,画出线段![]()
(3)填空:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
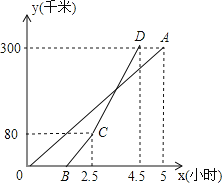
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),经多次测试后,得到如下部分数据:
x/米 | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | … |
y/米 | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | … |
(1)由表中的数据及函数学习经验,求出y关于x的函数解析式;
(2)试求出当乒乓球落在桌面时,其落点与端点A的水平距离是多少米?
(3)当乒乓球落在桌面上弹起后,y与x之间满足![]() .
.
①用含a的代数式表示k;
②已知球网高度为0.14米,球桌长(1.4×2)米.若a=-0.5,那么乒乓球弹起后,是否有机会在某个击球点可以将球沿直线扣杀到端点A?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
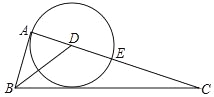
【题目】如图,在Rt△ABC中,∠BAC=90°,BD是角平分线,以点D为圆心,DA为半径的⊙D与AC相交于点E
(1)求证:BC是⊙D的切线;
(2)若AB=5,BC=13,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com