练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，求m的取值范围．

    分析 结合图象可得y≥-3，即ax2+bx≥-3，由ax2+bx+m=0可得ax2+bx=-m，则有-m≥-3，即可解决问题．

    解答 解：
    由图可知：y≥-3，即ax2+bx≥-3，
    ∵ax2+bx+m=0，
    ∴ax2+bx=-m，
    ∴-m≥-3，
    ∴m≤3．

    点评 本题主要考查抛物线与一元二次方程之间的关系、解一元一次不等式等知识，利用数形结合的思想是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．食品安全是老百姓关注的话题，在食品中添加过量的添加剂对人体有害，但适量的添加剂对人体无害且有利于食品的储存和运输．某饮料加工厂生产的A、B两种饮料均需加入同种添加剂，A饮料每瓶需加该添加剂0.4克，B饮料每瓶需加该添加剂0.5克，已知生产A、B两种饮料共100瓶恰好用了这种添加剂共46克．
    （1）A、B两种饮料各生产了多少瓶？
    （2）若该饮料加工厂想利用现有库存的102kg这种食品添加剂生产A、B两种饮料共10000箱（每箱24瓶），且根据市场营销情况，B种饮料的生产数量不少于A中饮料的$\frac{1}{4}$，该饮料加工厂应如何安排两种饮料的生产数量？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

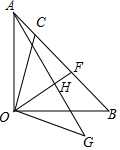    20．如图，△AOB为等腰直角三角形，∠AOB=90°，C是线段AB上一点，连接OC，作OG⊥OC，且OC=OG，连接AG，取CF=FB，连OF交AG于H，求证：OH⊥AG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

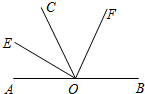    17．如图，O为直线AB上一点，作射线OC，OE平分∠AOC，OF平分∠BOC．
    （1）试判断OE与OF的位置关系，并说明理由；
    （2）若∠COF：∠EOB=2：5，求∠AOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，AD是△ABC的平分线，E为BC的中点，EF∥AB交AD于点F，CF的延长线交AB于点G，求证：AG=AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

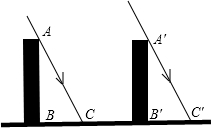    14．如图，太阳光线AC与A′C′是平行的，同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长，那么这辆跟木杆高度相同吗？
    小明思考过程如下：（请在括号内填上理由）
    因为AC∥A′C′．（①已知）
    所以∠ACB=∠A′C′B′．（②两直线平行，同位角相等）
    在△ABC和△A′B′C′中．
    因为∠ABC=∠A′B′C′=90°，BC=B′C′，∠ACB=∠A′C′B′．
    所以△ABC≌△A′B′C′．（③ASA）
    所以AB=A′B′（④全等三角形对应边相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，点E在BC上，点A、E、D在同一条直线上，AB⊥BC，CD⊥BC，若测得BE=20m，EC=10m，CD=20m，则河宽AB=（　　）
    A．60mB．40mC．30mD．20m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列运算正确的是（　　）
    A．$\sqrt{18}$$-\sqrt{2}$=2B．$\sqrt{14}$×$\sqrt{2}$=2$\sqrt{7}$C．（$\sqrt{3}+2）$2=7D．（-2ab2）3=-6a3b6

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知四边形ABCD是平行四边形，下列结论中不正确的是（　　）
    A．当AB=BC时，它是菱形B．当AC⊥BD时，它是菱形
    C．当∠ABC=90°时，它是矩形D．当AC=BD时，它是正方形

    查看答案和解析>>

    同步练习册答案