��1����һ�κ���y=
x+b��ͼ����B��-1��0����
��0=
����-1��+b��
���b=
��
��������y=-
x
2+
x+c������B��-1��0����
��0=-
����-1��
2+
����-1��+c��
���c=3��
��2����
x+
=-
x
2+
x+3��
�����x
2-2x-3=0��
��ã�x
1=-1��x
2=3��
��x=3ʱ��y=2��
��A��3��2����
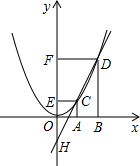
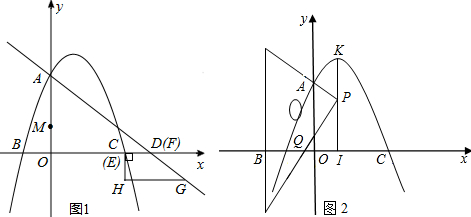
����ͼ1������A��AH��y����H��
��A��3��2����B��-1��0����D��0��3����
���ڡ�ABD�У�AB
2=��-1-3��
2+��0-2��
2=20��AD
2=��0-3��
2+��3-2��
2=10��DB
2=��-1-0��
2+��0-3��
2=10��
��AB
2=AD
2+DB
2��AD=DB��
���ABD�ǵ���ֱ�������Σ���ADB=90�㣬
�ߡ�ABD�����Բ��M��x���������ڵ�C��
��ABΪ��M��ֱ������ACB=90�㣬��ACD=��BCD=45�㣬
�֡ߡ�BDC=��BAC��
���DBC
����AEC��
���DBC=��AEC��
��tan��AEC=tan��DBC=
=
=3��
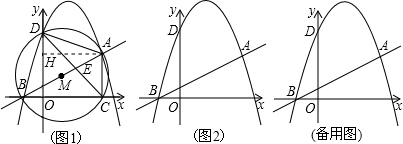
��3����Ϊ3�����������ת��OD���������ϣ�����ת��OB���������ϣ�����ת��BD���������ϣ�
1����ת��OD���������ϣ�
��ΪO��D�䣬��O��D��ƽ����x�ᣬ������y=-
x
2+
x+3=-
��x-
��
2+
���Գ���x=
��
��x
1=
-
|OD|=
-
=-
��x
2=
+
=
��
��������-
��
������
��
����
��ʱ�ֱ𣺢�O�䣨-
��
����D�䣨
��
������O�䣨
��
����D�䣨-
��
������ʱO��D��=3��
����ת����P�������Ϊ��x��y����
�����O�䣨-
��
����D�䣨
��
���������⣬��
�����
��
��ʱ��ת����P
1��
��
����
�����O�䣨
��
����D�䣨-
��
���������⣬��
�����
��
��ʱ��ת����P
2��
��
����
2����ת��OB���������ϣ�
����OB��y�ᣬ��O��B���x�ᣬ��ʱ��Ȼ��������
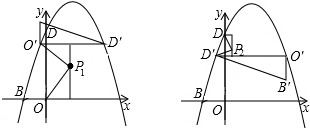
3����ת��BD���������ϣ�
BD����ת90��������߶�B��D����BD��ֱ��ֱ��б��k
BD=3����k
B��D��=-
��
����ת��B��D������ֱ�߷���Ϊ��y=-
x+m��
�������ߣ�y=-
x
2+
x+3�������ⷽ���飬�ã�
��
����Ϊ������������꣮
��B��D��=BD=
��
�ࣨ
-
��
2+��
-
��
2=10��
��������585-120m=225��
���m=3��
���������꣺��3��2������0��3����
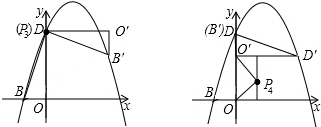
�����B�䣨3��2����D�䣨0��3������D����D�غϣ����Դ�ʱ��ת����ΪP
3��0��3����
�����D�䣨3��2����B�䣨0��3�������ʱ��ת����ΪP
4��1��1����
���Ͽ�֪����ת����Ϊ��0��3������1��1������
��
������
��
����


 ��2����
��2���� ��ʱ�ֱ𣺢�O�䣨-
��ʱ�ֱ𣺢�O�䣨- 3����ת��BD���������ϣ�
3����ת��BD���������ϣ�

 �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
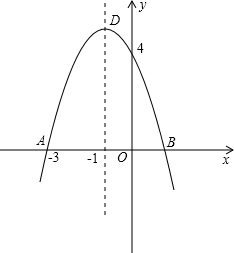 ��-3��0����
��-3��0����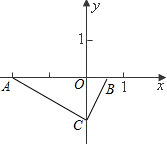
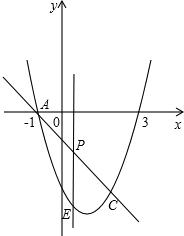 C���㣬����C��ĺ�����Ϊ2��
C���㣬����C��ĺ�����Ϊ2��