
 如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=72°.
如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ=72°. 分析 连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.
解答 解:连接OA、OB、OC,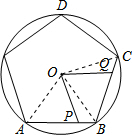
∵五边形ABCDE是⊙O的内接正五边形,
∴∠AOB=∠BOC=72°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=54°,
在△OBP和△OCQ中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBP=∠OCQ}\\{BP=CQ}\end{array}\right.$,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=72°.
故答案为:72°.
点评 本题考查的是正多边形和圆、全等三角形的判定和性质,掌握正多边形的中心角的求法、全等三角形的判定定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
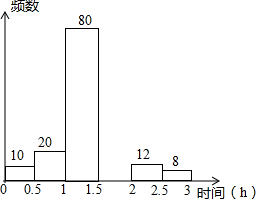 为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:
为养成学生课外阅读的习惯,各学校普遍开展了“我的梦 中国梦”课外阅读活动.某校为了解七年级1200名学生课外日阅读所用时间情况,从中随机抽查了部分同学,进行了相关统计,整理并绘制出如下不完整的频数分布表和频数分布直方图,请根据图表信息解答下列问题:| 组别 | 时间段(小时) | 频数 | 频率 |
| 1 | 0≤x<0.5 | 10 | 0.05 |
| 2 | 0.5≤x<1.0 | 20 | 0.10 |
| 3 | 1.0≤x<1.5 | 80 | b |
| 4 | 1.5≤x<2.0 | a | 0.35 |
| 5 | 2.0≤x<2.5 | 12 | 0.06 |
| 6 | 2.5≤x<3.0 | 8 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 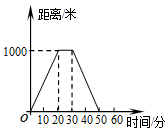 | B. | 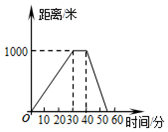 | ||
| C. | 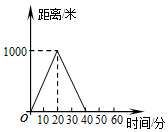 | D. | 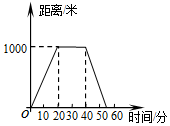 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
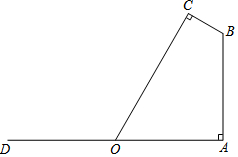 如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1×106 | B. | 100×104 | C. | 1×107 | D. | 0.1×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
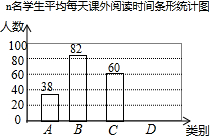 某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.
某校开展“百日读书好习惯”活动,校团委为了解学生每天课外阅读情况,随机抽取了n名学生,统计他们平均每天课外阅读时间(单位:时)根据时间的长短分为A,B,C,D四类,并将所得数据绘制成如下统计表及不完整的统计图.| 类别 | 时间t(小时) | 人数 |
| A | 0<t≤0.5 | 38 |
| B | 0.5<t≤1 | 82 |
| C | 1<t≤1.5 | 60 |
| D | t>1.5 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com