练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

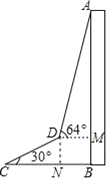
    【题目】为了测量出大楼AB的高度，从距离楼底B处50米的点C（点C与楼底B在同一水平面上）出发，沿倾斜角为30°的斜坡CD前进20米到达点D，在点D处测得楼顶A的仰角为64°，求大楼AB的高度（结果精确到1米）（参考数据：sin64°≈0.9，cos64°≈0.4，tan64°≈2.1， ≈1.7）

    【答案】楼AB的高度约为79米．

    【解析】试题分析：在Rt△CDN中求得BM=DN=CD=10、CN=CDcos∠C=10，即可知DM=BN=50﹣10，根据AB=BM+AM=BM+DMtan∠ADN可得答案．

    试题解析：在Rt△CDN中，∵CD=20米，∠C=30°，

    ∴BM=DN=CD=10米，CN=CDcos∠C=20×=10米，

    ∵BC=50米，

    ∴DM=BN=BC﹣CN=50﹣10，

    在Rt△ADN中，由tan∠ADN= 可得AM=DMtan∠ADN=（50﹣10）tan64°，

    则AB=AM+BM=（50﹣10）tan64°+10≈79米，

    答：楼AB的高度约为79米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】有甲、乙两筐水果,甲筐水果的质量为(m-1)2kg,乙筐水果的质量为(m2-1)kg(其中m>1),售完后,两筐水果都卖了120元.
    （1）哪筐水果的单价高?
    （2）高的单价是低的单价的多少倍?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝2，BC＝1，动点P从点B出发，沿路线B→C→D作匀速运动，那么△APB的面积S与点P运动的路程之间的函数图象大致是（ ）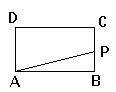

    A.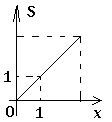
    B.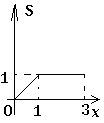
    C.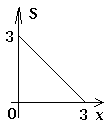
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．

    （1）如图①，若∠BAC=23°，求∠AMB的大小；

    （Ⅱ）如图②，过点B作BD∥MA，交AC于点E，交⊙O于点D，若BD=MA，求∠AMB的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，若∠AOB=∠ACB=90°，OC平分∠AOB.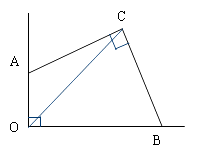

    （1）你能将四边形AOBC通过剪裁拼成一个正方形吗？画出裁剪方法并有必要的说明。
    （2）若OC=2，你能求出四边形AOBC的面积吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD平分∠BAC，过AD的中点O作EF⊥AD，分别交AB、AC于点E、F，连接DE、DF．

    （1）判断四边形AFDE是什么四边形？请说明理由；

    （2）若BD=8，CD=3，AE=4，求CF的长．

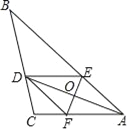
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（﹣1，0）．下列结论：

    ①ac＜0；②4a﹣2b+c＞0；③抛物线与x轴的另一个交点是（4，0）；

    ④点（﹣3，y1），（6，y2）都在抛物线上，则有y1＜y2．其中正确的个数为（　　）

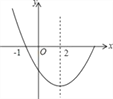
    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△DBE中，BC=BE，还需再添加两个条件才能使△ABC≌△DBE，则不能添加的一组条件是（ ）

    A.AB=DB，∠ A=∠ D
    B.DB=AB，AC=DE
    C.AC=DE，∠C=∠E
    D.∠ C=∠ E，∠ A=∠ D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点P（m﹣1，2m+1）在第一象限，则m的取值范围是 ．

    查看答案和解析>>

    同步练习册答案