
【题目】如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照下图并思考,完成下列各题.
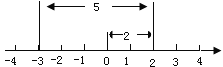
(1)如果点A表示的数-1,将点A向右移动4个单位长度,那么终点B表示的数是____.A、B两点间的距离是__________.
(2)如果点A表示的数2,将点A向左移动6个单位长度,再向右移动3个单位长度,那么终点B表示的数是____.A、B两点间的距离是____.
(3)如果点A表示的数m,将点A向左移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是___.A、B两点间的距离是______.
科目:初中数学 来源: 题型:
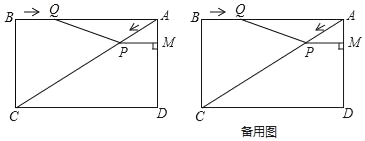
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
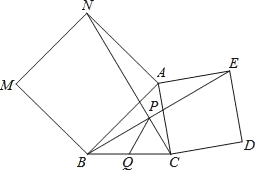
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
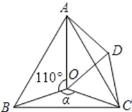
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在平面直角坐标系中,点A在y轴正半轴上,点B、C分别在x轴的负半轴、正半轴上,且AB=AC,∠ACB=30°,OD⊥AB于点D.
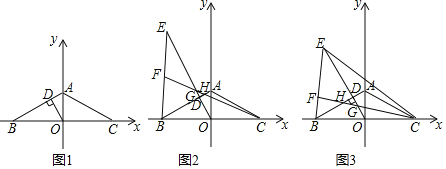
(1)求证:BD=3AD;
(2)如图2,点E在OD的延长线上,连接BE,在线段BE上取点F,连接CF分别交OE、AB于点G、H(点G、H、D互不重合),若FE=FG,求证:∠EBA﹣∠BCF的度数为定值;
(3)如图3,在(2)的条件下,连接EC,若C(4![]() ,0),A(0,4),求S△ECG.
,0),A(0,4),求S△ECG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校初一(2)班组织学生从A地到B地步行野营,匀速前进,该班师生共56人,每8人排成一排,相邻两排之间间隔1米,途中经过一座桥CD,队伍从开始上桥到刚好完全离开桥共用了150秒,当队尾刚好走到桥的一端D处时,排在队尾的游班长发现小蒋还在桥的另一端C处拍照,于是以队伍1.5倍的速度返回去找小萍,同时队伍仍按原速度继续前行,30秒后,小蒋发现游班长返回来找他,便立刻以2.1米/秒的速度向游班长方向行进,小蒋行进40秒后与游班长相遇,相遇后两人以队伍2倍的速度前行追赶队伍.
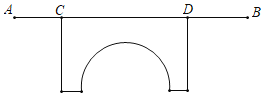
(1)初一(2)班的队伍长度为 米;
(2)求班级队伍行进的速度(列一元一次方程解决问题);
(3)请问:游班长从D处返回赵小萍开始到他们两人追上队首的刘老师一共用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
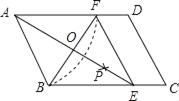
【题目】如图,在ABCD中,AB<BC,以点A为圆心,AB长为半径作圆弧交AD于点F,再分别以点B、F为圆心,大于BF的一半长为半径作圆弧,两弧交于一点P,连结AP并延长交BC于点E,连结EF.
(1)四边形ABEF是_____(填“矩形”、“菱形”、“正方形”或“无法确定”)(直接填写结果),并证明你的结论.
(2)AE、NF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为_____,∠ADC=_____°,(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
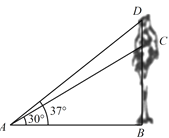
【题目】九(1)班课题学习小组,为了了解大树生长状况,去年在学校门前点 ![]() 处测得一棵大树顶点
处测得一棵大树顶点 ![]() 的仰角为
的仰角为 ![]() ,树高
,树高 ![]() .今年他们仍在原点
.今年他们仍在原点 ![]() 处测得树顶点
处测得树顶点 ![]() 的仰角为
的仰角为 ![]() ,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据:
,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
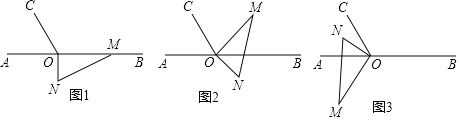
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况.在旋转的过程中,当第t秒时,三条射线OA、OC、OM构成相等的角,求此时t的值;
(3)将图1中的三角板绕点O逆时针旋转至图3,使ON在∠AOC的内部时,请探究∠AOM与∠CON的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com