
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
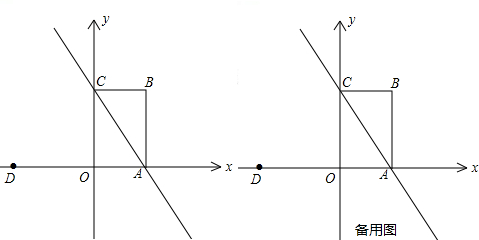
已知在平面直角坐标系中,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D的坐标为
,点D的坐标为![]() ,点P是直线AC上的一动点,直线DP与
,点P是直线AC上的一动点,直线DP与![]() 轴交于点M.问:
轴交于点M.问:
(1)当点P运动到何位置时,直线DP平分矩形OABC的面积,请简要说明理由,并求出此时直线DP的函数解析式;
(2)当点P沿直线AC移动时,是否存在使![]() 与
与![]() 相似的点M,若存在,请求出点M的坐标;若不存在,请说明理由;
相似的点M,若存在,请求出点M的坐标;若不存在,请说明理由;
(3)当点P沿直线AC移动时,以点P为圆心、半径长为R(R>0)画圆,所得到的圆称为动圆P.若设动圆P的直径长为AC,过点D作动圆P的两条切线,切点分别为点E、F.请探求是否存在四边形DEPF的最小面积S,若存在,请求出S的值;若不存在,请说明理由.
注:第(3)问请用备用图解答.
 |
查看答案和解析>>
科目:初中数学 来源:云南省中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市昌平区九年级第一学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数y=x2–kx+k–1(k>2).

(1)求证:抛物线y=x2–kx+k-1(k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与 相离、相切、相交.
相离、相切、相交.
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com