
分析 (1)根据题中所给材料,求出零点值;
(2)将全体实数分成不重复且不遗漏的三种情况解答;
(3)由|x+2|+|x-4|=6,得到-2≤x≤4,于是得到结果;
(4)|x+2|+|x-4|有最小值,通过x的取值范围即可得到结果.
解答 解:(1)∵|x+2|和|x-4|的零点值,可令x+2=0和x-4=0,解得x=-2和x=4,
∴-2,4分别为|x+2|和|x-4|的零点值.
(2)当x<-2时,|x+2|+|x-4|=-2x+2;
当-2≤x<4时,|x+2|+|x-4|=6;
当x≥4时,|x+2|+|x-4|=2x-2;
(3)∵|x+2|+|x-4|=6,
∴-2≤x≤4,
∴整数解为:-2,-1,0,1,2,3,4.
(4)|x+2|+|x-4|有最小值,
∵当x=-2时,|x+2|+|x-4|=6,
当x=4时,|x+2|+|x-4|=6,
∴|x+2|+|x-4|的最小值是6.
点评 本题主要考查了绝对值,解题的关键是能根据材料所给信息,找到合适的方法解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增加/辆 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
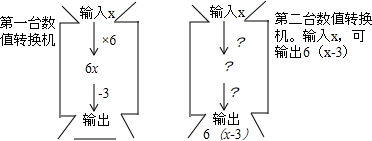
| 输入 | -2 | -$\frac{1}{2}$ | 0 | 0.26 | $\frac{1}{3}$ | $\frac{5}{2}$ | 4.5 |
| 第一台的输出 | -15 | -6 | -3 | -1.44 | -2 | 12 | 24 |
| 第二台的输出 | -30 | -9 | -18 | -16.44 | -16 | -3 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
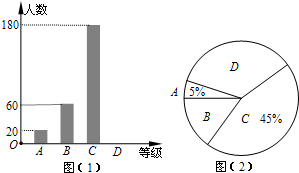 某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.
某报社为了解宿迁市民对大范围雾霾天气的成因、影响以及应对措施的看法,做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.请结合统计图表,回答下列问题.| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | m |
| C.基本了解 | 45% |
| D.不了解 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com