
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6).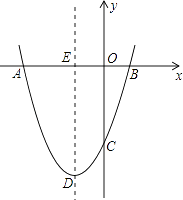
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx+c经过点A(﹣6,0),B(2,0),C(0,﹣6),
∴  ,解得
,解得  .
.
∴抛物线的解析式为:y= ![]() x2+2x﹣6
x2+2x﹣6
(2)
解:如图,过点P作x轴的垂线,交AC于点N.

设直线AC的解析式为y=kx+m,由题意,得
![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为:y=﹣x﹣6.
设P点坐标为(x, ![]() x2+2x﹣6),则点N的坐标为(x,﹣x﹣6),
x2+2x﹣6),则点N的坐标为(x,﹣x﹣6),
∴PN=PE﹣NE=﹣( ![]() x2+2x﹣6)+(﹣x﹣6)=﹣
x2+2x﹣6)+(﹣x﹣6)=﹣ ![]() x2﹣3x.
x2﹣3x.
∵S△PAC=S△PAN+S△PCN,
∴S= ![]() PNOA=
PNOA= ![]() ×6(﹣
×6(﹣ ![]() x2﹣3x)=﹣
x2﹣3x)=﹣ ![]() (x+3)2+
(x+3)2+ ![]() ,
,
∴当x=﹣3时,S有最大值 ![]() ,此时点P的坐标为(﹣3,﹣
,此时点P的坐标为(﹣3,﹣ ![]() )
)
(3)
解:在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y= ![]() x2+2x﹣6=
x2+2x﹣6= ![]() (x+2)2﹣8,
(x+2)2﹣8,
∴顶点D的坐标为(﹣2,﹣8),
∵A(﹣6,0),
∴AD2=(﹣2+6)2+(﹣8﹣0)2=80.
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图3①,
由勾股定理,得AM2+AD2=DM2,
即(0+6)2+(t﹣0)2+80=(0+2)2+(t+8)2,
解得t=3,
所以点M的坐标为(0,3);
②当D为直角顶点时,如图3②,
由勾股定理,得DM2+AD2=AM2,
即(0+2)2+(t+8)2+80=(0+6)2+(t﹣0)2,
解得t=﹣7,
所以点M的坐标为(0,﹣7);
③当M为直角顶点时,如图3③,
由勾股定理,得AM2+DM2=AD2,
即(0+6)2+(t﹣0)2+(0+2)2+(t+8)2=80,
解得t=﹣2或﹣6,
所以点M的坐标为(0,﹣2)或(0,﹣6);
综上可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0,3)或(0,﹣7)或(0,﹣2)或(0,﹣6)



【解析】(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x, ![]() x2+2x﹣6),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.
x2+2x﹣6),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线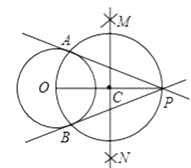
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有 .
①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0.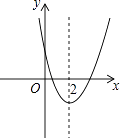
查看答案和解析>>
科目:初中数学 来源: 题型:
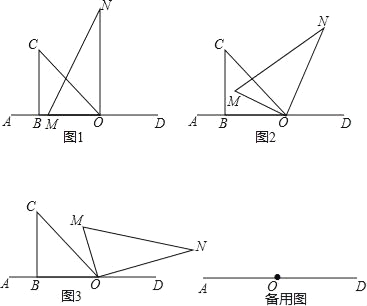
【题目】将一副直角三角板按如图1 摆放在直线AD 上(直角三角板OBC 和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC 不动,将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒.
(1)如图2,当t= 秒时,OM 平分∠AOC,此时∠NOC﹣∠AOM= ;
(2)继续旋转三角板MON,如图3,使得OM、ON 同时在直线OC 的右侧,猜想∠NOC与∠AOM 有怎样的数量关系?并说明理由(数量关系中不能含t);
(3)直线AD 的位置不变,若在三角板MON 开始顺时针旋转的同时,另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转,当OM 旋转至射线OD 上时,两个三角板同时停止运动.
①当t= 秒时,∠MOC=15°;
②请直接写出在旋转过程中,∠NOC 与∠AOM 的数量关系(数量关系中不能含t).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图,解答下列问题.
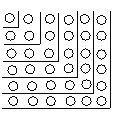
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续
下去,那么第七层有几个小圆圈?第n层呢?
(2)某一层上有77个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1 + 3 = 22.
同样,
由前三层的圆圈个数和得:1 + 3 + 5 = 32.
由前四层的圆圈个数和得:1 + 3 + 5 + 7 = 42.
由前五层的圆圈个数和得:1 + 3 + 5 + 7 + 9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1 + 3 + 5 + … + 19的和;
(5)计算:11 + 13 + 15 + … + 99的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
(1)统计表中的m= ,n= ;
(2)补全条形统计图;

(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的![]() 还多1岁.
还多1岁.
(1)请用含m的式子表示这三人的年龄和;
(2)若这三人的年龄和为35岁,请你求出这三人的年龄.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂质检部门对一批水果罐头的质量进行检查,从中随意抽查了10个,净含量如下(单位:g):339,343,341,347,345,341,340,344,329,341.
(1)这个问题中,总体、个体、样本各是什么?
(2)试估计出这批水果罐头的平均质量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com