
ЁОЬтФПЁПзїЭМгыЬНОПЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЌВЂгУ 0.5 КСУзКкЩЋЧЉзжБЪУшЩюКлМЃЃЉ ШчЭМЃЌЁЯDBC КЭЁЯECB ЪЧЁїABC ЕФСНИіЭтНЧЁу
(1)гУжБГпКЭдВЙцЗжБ№зїЁЯDBC КЭЁЯECB ЕФЦНЗжЯпЃЌЩшЫќУЧЯрНЛгкЕу PЃЛ
(2)Й§Еу P ЗжБ№ЛжБЯп ABЁЂACЁЂBC ЕФДЙЯпЖЮ PMЁЂPNЁЂPQЃЌДЙзу ЮЊ MЁЂNЁЂQЃЛ
(3) PMЁЂPNЁЂPQ ЯрЕШТ№ЃПЃЈжБНгаДГіНсТлЃЌВЛашЫЕУїРэгЩЃЉ

ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉМћНтЮіЃЈ3ЃЉжЄУїМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЃЈ2ЃЉАДвЊЧѓзїЭММДПЩЃЎ
ЃЈ3ЃЉPMЁЂPNЁЂPQЯдШЛЪЧЯрЕШЕФЃЌдкЁЯDBCжаЃЌгЩгкBPЪЧЁЯDBCЕФНЧЦНЗжЯпЃЌЖјЕуPдкЩфЯпBPЩЯЃЌЧвPMЁЂPQЗжБ№ДЙжБгкЁЯDBCЕФСНБпЃЌИљОнНЧЦНЗжЯпЕФаджЪЃЌМДПЩЕУPM=PQЃЌЭЌРэПЩжЄPN=PQЃЌгЩДЫЕУЕНЫљЧѓЕФНсТл
(1)ШчЯТЭМЃЎ
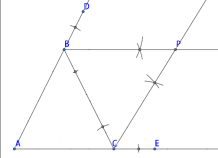
(2)ШчЯТЭМЃЎ
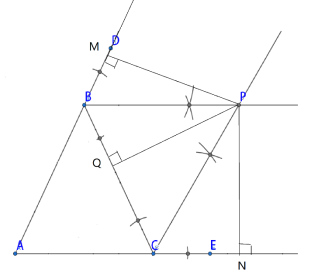
ЃЈ3ЃЉPM=PN=PQЃЎ
РэгЩЃКгЩгкBPЪЧЁЯDBCЕФНЧЦНЗжЯпЃЌЧвPMЁЭBDЁЂPQЁЭBCЃЌИљОнНЧЦНЗжЯпЕФаджЪЕУЃКPM=PQЃЌЭЌРэЃЌPQ=PNЃЛ
ЙЪPM=PN=PQ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЮЊСЫЮќв§ЙЫПЭЃЌЩшСЂСЫвЛИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЌШчЭМЫљЪОЃЌВЂЙцЖЈЃКЙЫПЭЯћЗб200дЊЃЈКЌ200дЊЃЉвдЩЯЃЌОЭФмЛёЕУвЛДЮзЊЖЏзЊХЬЕФЛњЛсЃЌШчЙћзЊХЬЭЃжЙКѓЃЌжИеые§КУЖдзМОХелЁЂАЫелЁЂЦпелЧјгђЃЌЙЫПЭОЭПЩвдЛёЕУДЫЯюгХЛнЃЌШчЙћжИеыЧЁКУдкЗжИюЯпЩЯЪБЃЌдђашжиаТзЊЖЏзЊХЬ.
ЃЈ1ЃЉФГЙЫПЭе§КУЯћЗб220дЊЃЌЫћзЊвЛДЮзЊХЬЃЌЫћЛёЕУОХелЁЂАЫелЁЂЦпелгХЛнЕФИХТЪЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉФГЙЫПЭЯћЗбжаЛёЕУСЫзЊЖЏвЛДЮзЊХЬЕФЛњЛсЃЌЪЕМЪИЖЗб168дЊЃЌЧыЮЪЫћЯћЗбЫљЙКЮяЦЗЕФдМлгІЮЊЖрЩйдЊ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() .ЕуOЪЧBCЕФжаЕуЃЌЕуDбиBЁњAЁњCЗНЯђДгBдЫЖЏЕНCЃЎЩшЕуDОЙ§ЕФТЗОЖГЄЮЊ
.ЕуOЪЧBCЕФжаЕуЃЌЕуDбиBЁњAЁњCЗНЯђДгBдЫЖЏЕНCЃЎЩшЕуDОЙ§ЕФТЗОЖГЄЮЊ![]() ЃЌЭМ1жаФГЬѕЯпЖЮЕФГЄЮЊyЃЌШєБэЪОyгыxЕФКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓШчЭМ2ЫљЪОЃЌдђетЬѕЯпЖЮПЩФмЪЧЭМ1жаЕФЃЈЁЁЁЁЃЉ
ЃЌЭМ1жаФГЬѕЯпЖЮЕФГЄЮЊyЃЌШєБэЪОyгыxЕФКЏЪ§ЙиЯЕЕФДѓжТЭМЯѓШчЭМ2ЫљЪОЃЌдђетЬѕЯпЖЮПЩФмЪЧЭМ1жаЕФЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭъШЋЦНЗНЙЋЪНЃКЃЈaЁРbЃЉ2ЃНa2ЁР2ab+b2ЪЪЕБЕФБфаЮЃЌПЩвдНтОіКмЖрЕФЪ§бЇЮЪЬтЃЎ
Р§ШчЃКШєa+bЃН3ЃЌabЃН1ЃЌЧѓa2+b2ЕФжЕЃЎ
НтЃКвђЮЊa+bЃН3ЃЌabЃН1
ЫљвдЃЈa+bЃЉ2ЃН9ЃЌ2abЃН2
Ыљвдa2+b2+2abЃН9ЃЌ2abЃН2
ЕУa2+b2ЃН7
ИљОнЩЯУцЕФНтЬтЫМТЗгыЗНЗЈЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉШєЃЈ7ЉxЃЉЃЈxЉ4ЃЉЃН1ЃЌЧѓЃЈ7ЉxЃЉ2+ЃЈxЉ4ЃЉ2ЕФжЕЃЛ
ЃЈ2ЃЉШчЭМЃЌЕуCЪЧЯпЖЮABЩЯЕФвЛЕуЃЌвдACЁЂBCЮЊБпЯђСНБпзїе§ЗНаЮЃЌЩшABЃН5ЃЌСНе§ЗНаЮЕФУцЛ§КЭS1+S2ЃН17ЃЌЧѓЭМжавѕгАВПЗжУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаДѓаЁСНжжЛѕГЕЃЌ3СОДѓЛѕГЕгы2СОаЁЛѕГЕвЛДЮПЩвддЫЛѕ21ЖжЃЌ2СОДѓЛѕГЕгы4СОаЁЛѕГЕвЛДЮПЩвддЫЛѕ22ЖжЃЎ
ЃЈ1ЃЉУПСОДѓЛѕГЕКЭУПСОаЁЛѕГЕвЛДЮИїПЩвддЫЛѕЖрЩйЖжЃП
ЃЈ2ЃЉЯжгаетСНжжЛѕГЕЙВ10СОЃЌвЊЧѓвЛДЮдЫЛѕВЛЕЭгк35ЖжЃЌдђЦфжаДѓЛѕГЕжСЩйЖрЩйСОЃПЃЈгУВЛЕШЪННтД№ЃЉ
ЃЈ3ЃЉШеЧАга23ЖжЛѕЮяашвЊдЫЪфЃЌгћзтгУетСНжжЛѕГЕдЫЫЭЃЌвЊЧѓШЋВПЛѕЮявЛДЮдЫЭъЧвУПСОГЕБиаызАТњЃЎвбжЊУПСОДѓЛѕГЕвЛДЮдЫЛѕзтН№ЮЊ300дЊЃЌУПСОаЁЛѕГЕвЛДЮдЫЛѕзтН№ЮЊ200дЊЃЌЧыСаГіЫљгаЕФдЫЪфЗНАИОЎЧѓГізюЩйзтН№ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ CD ЪЧОЙ§ЁЯBCA ЖЅЕу C ЕФвЛЬѕжБЯпЃЌCAЃНCBЃЎEЁЂF ЗжБ№ЪЧжБЯп CD ЩЯСНЕуЃЈВЛ жиКЯЃЉЃЌЧвЁЯBECЃНЁЯCFAЃНЁЯa
(1)ШєжБЯп CD ОЙ§ЁЯBCA ЕФФкВПЃЌЧв EЁЂF дкЩфЯп CD ЩЯЃЌЧыНтОіЯТУцЮЪЬтЃК
ЂйШєЁЯBCAЃН90ЁуЃЌЁЯaЃН90ЁуЃЌЧыдкЭМ 1 жаВЙШЋЭМаЮЃЌВЂжЄУїЃКBEЃНCFЃЌEFЃН![]() ЃЛ
ЃЛ
ЂкШчЭМ 2ЃЌШє 0Ёу<ЁЯBCA<180ЁуЃЌЧыЬэМгвЛИіЙигкЁЯa гыЁЯBCA ЙиЯЕЕФЬѕМў ЃЌ ЪЙЂйжаЕФСНИіНсТлШдШЛГЩСЂЃЛ
(2)ШчЭМ 3ЃЌШєжБЯп CD ОЙ§ЁЯBCA ЕФЭтВПЃЌЁЯaЃНЁЯBCAЃЌЧыаДГі EFЁЂBEЁЂAF Ш§ЬѕЯп ЖЮЪ§СПЙиЯЕЃЈВЛвЊЧѓжЄУїЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃКдкЪ§жсЩЯ![]() гы
гы![]() ЫљЖдЕФСНЕужЎМфЕФОрРыЃК
ЫљЖдЕФСНЕужЎМфЕФОрРыЃК![]() ЃЛ
ЃЛ
дкЪ§жсЩЯ![]() гы
гы![]() ЫљЖдЕФСНЕужЎМфЕФОрРыЃК
ЫљЖдЕФСНЕужЎМфЕФОрРыЃК![]() ЃЛ
ЃЛ
дкЪ§жсЩЯ![]() гы
гы![]() ЫљЖдЕФСНЕужЎМфЕФОрРыЃК
ЫљЖдЕФСНЕужЎМфЕФОрРыЃК![]() ЃЛ
ЃЛ
дкЪ§жсЩЯЕу![]() ЁЂ
ЁЂ![]() ЗжБ№БэЪОЪ§
ЗжБ№БэЪОЪ§![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЁЂ
ЁЂ![]() СНЕужЎМфЕФОрРы
СНЕужЎМфЕФОрРы![]() ЃЎ
ЃЎ
ЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ![]() ЃЉЪ§жсЩЯБэЪО
ЃЉЪ§жсЩЯБэЪО![]() КЭ
КЭ![]() ЕФСНЕужЎМфЕФОрРыЪЧ__________ЃЎ
ЕФСНЕужЎМфЕФОрРыЪЧ__________ЃЎ
Ъ§жсЩЯБэЪОЪ§![]() КЭ
КЭ![]() ЕФСНЕужЎМфЕФОрРыБэЪОЮЊ__________ЃЎЪ§жсЩЯБэЪОЪ§__________КЭ__________ЕФСНЕужЎМфЕФОрРыБэЪОЮЊ
ЕФСНЕужЎМфЕФОрРыБэЪОЮЊ__________ЃЎЪ§жсЩЯБэЪОЪ§__________КЭ__________ЕФСНЕужЎМфЕФОрРыБэЪОЮЊ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЦпФъМЖбаОПадбЇЯАаЁзщдкЪ§бЇРЯЪІжИЕМЯТЃЌЖдЪНзгНјааЬНОПЃК
ЃЉЦпФъМЖбаОПадбЇЯАаЁзщдкЪ§бЇРЯЪІжИЕМЯТЃЌЖдЪНзгНјааЬНОПЃК![]() ЃЎ
ЃЎ
ЂйЧыФудкВнИхжНЩЯЛГіЪ§жсЃЌЕББэЪОЪ§![]() ЕФЕудк
ЕФЕудк![]() гы
гы![]() жЎМфвЦЖЏЪБЃЌ
жЎМфвЦЖЏЪБЃЌ![]() ЕФжЕзмЪЧвЛИіЙЬЖЈЕФжЕЮЊЃК__________ЃЎЃЈжБНгаДГіНсЙћЃЉ
ЕФжЕзмЪЧвЛИіЙЬЖЈЕФжЕЮЊЃК__________ЃЎЃЈжБНгаДГіНсЙћЃЉ
ЂкЧыФудкВнИхжНЩЯЛГіЪ§жсЃЌвЊЪЙ![]() ЃЌЪ§жсЩЯТњзуЬѕМўЕФЕуБэЪОЕФЪ§зжЪЧЃК__________ЃЈжБНгаДГіНсЙћЃЉЃЎ
ЃЌЪ§жсЩЯТњзуЬѕМўЕФЕуБэЪОЕФЪ§зжЪЧЃК__________ЃЈжБНгаДГіНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOЪЧЁїABCФквЛЕуЃЌСЌНсOBЁЂOCЃЌВЂНЋABЁЂOBЁЂOCЁЂACЕФжаЕуDЁЂEЁЂFЁЂGвРДЮСЌНсЃЌЕУЕНЫФБпаЮDEFGЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮDEFGЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЙћЁЯOBC=45ЁуЃЌЁЯOCB=30ЁуЃЌOC=4ЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁѕABCDжаЃЌЕуEЪЧБпADЩЯвЛЕуЃЌЧвAE=ABЃЎ
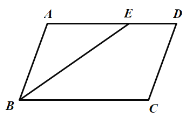
ЃЈ1ЃЉзїЁЯBCDЕФНЧЦНЗжЯпCFЃЌНЛADгкFЕуЃЌНЛBEгкGЕуЃЛЃЈГпЙцзїЭМЃЌБЃСєКлМЃЃЌВЛаДЛЗЈЃЉ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌ
ЂйЧѓЁЯBGCЕФЖШЪ§ЃЛ
ЂкЩшAB=aЃЌBC=bЃЌдђЯпЖЮEF= ЃЈгУКЌa,bЕФЪНзгБэЪОЃЉЃЛ
ЂлШєAB=10ЃЌCF=12ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com