
【题目】已知点A(a,3),点B(b,6),点C(5,c),AC⊥x轴,CB⊥y轴,OB在第二象限的角平分线上:
(1)写出A,B,C三点坐标;
(2)求△ABC的面积;
(3)若点P为线段OB上动点,当△BCP面积大于12小于16时,求点P横坐标取值范围.
【答案】
(1)解:如图所示:
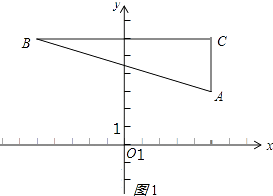
∵AC⊥x轴,CB⊥y轴,
∴A和C的横坐标相同,B和C的纵坐标相同,
∴A(5,3),C(5,6),
∵B在第二象限的角平分线上,
∴B(﹣6,6);
(2)解:∵BC=5﹣(﹣6)=11,
∴△ABC的面积= ![]() ×11×(6﹣3)=
×11×(6﹣3)= ![]() ;
;
(3)解:设P的坐标为(a,﹣a),
则△BCP的面积= ![]() ×11×(6+a),
×11×(6+a),
∵△BCP面积大于12小于16,
∴12< ![]() ×11×(6+a)<16,
×11×(6+a)<16,
解得:﹣ ![]() <a<﹣
<a<﹣ ![]() ;
;
即点P横坐标取值范围为:﹣ ![]() <a<﹣
<a<﹣ ![]() .
.

【解析】①根据题意得出A和C的横坐标相同,B和C的纵坐标相同,得出A(5,3),C(5,6),由角平分线的性质得出B的坐标;
②求出BC=5-(-6)=11,即可得出△ABC的面积;
③设P的坐标为(a,-a),则△BCP的面积=0.5×11(6+a),根据题意得出不等式12<0.5×11×(6+a)<16,解不等式即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某班抽查25名学生数学测验成绩(单位:分),频数分布直方图如图:
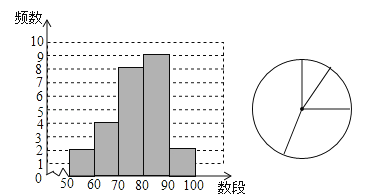
(1)成绩x在什么范围的人数最多?是多少人?
(2)若用半径为2的扇形图来描述,成绩在60≤x<70的人数对应的扇形面积是多少?
(3)从相成绩在50≤x<60和90≤x<100的学生中任选2人.小李成绩是96分,用树状图或列表法列出所有可能结果,求小李被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问从第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调x人,则可列方程( )
A.22+x=2×26
B.22+x=2(26-x)
C.2(22+x)=26-x
D.22=2(26-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1

表2

(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com