
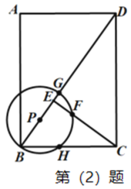
【题目】如图,在矩形 ABCD 中,CE⊥BD,AB=4,BC=3,P 为 BD 上一个动点,以 P 为圆心,PB 长半径作⊙P,⊙P 交 CE、BD、BC 交于 F、G、H(任意两点不重合),
(1)半径 BP 的长度范围为 ;
(2)连接 BF 并延长交 CD 于 K,若 tan KFC 3 ,求 BP;
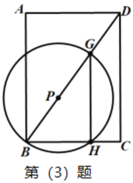
(3)连接 GH,将劣弧 HG 沿着 HG 翻折交 BD 于点 M,试探究![]() 是否为定值,若是求出该值,若不是,请说明理由.
是否为定值,若是求出该值,若不是,请说明理由.
【答案】(1)![]() ;(2)BP=1;(3)
;(2)BP=1;(3)![]()
【解析】
(1)当点G和点E重合,当点G和点D重合两种临界状态,分别求出BP的值,因为任意点都不重合,所以BP在两者之间即可得出答案;
(2)∠KFC和∠BFE是对顶角,得到![]() ,得出EF的值,再根据△BEF∽△FEG,求出EG的值,进而可求出BP的值;
,得出EF的值,再根据△BEF∽△FEG,求出EG的值,进而可求出BP的值;
(3)设圆的半径,利用三角函数表示出PO,GO的值,看![]() 用面积法求出
用面积法求出![]() ,在
,在![]() 中由勾股定理得出MQ的值,进而可求出PM的值即可得出答案.
中由勾股定理得出MQ的值,进而可求出PM的值即可得出答案.
(1)当G点与E点重合时,BG=BE,如图所示:
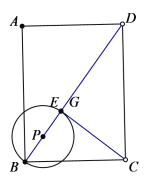
∵四边形ABCD是矩形,AB=4,BC=3,
∴BD=5,
∵CE⊥BD,
∴![]() ,
,
∴![]() ,
,
在△BEC中,由勾股定理得:
![]() ,
,
∴![]() ,
,
当点G和点D重合时,如图所示:

∵△BCD是直角三角形,
∴BP=DP=CP,
∴![]() ,
,
∵任意两点都不重合,
∴![]() ,
,
(2)连接FG,如图所示:
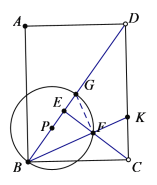
∵∠KFC=∠BFE,tan KFC 3,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵BG是圆的直径,
∴∠BFG=90°,
∴∠GFE+∠BFE=90°,
∵CE⊥BD,
∴∠FEG=∠FEB=90°,
∴∠GFE+∠FGE=90°,
∴∠BFE=∠FGE
∴△BEF∽△FEG,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴BG=EG+BE=2,
∴BP=1,
(3)![]() 为定值,
为定值,
过![]() 作
作![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交GH于点O,如下图所示:
交GH于点O,如下图所示:
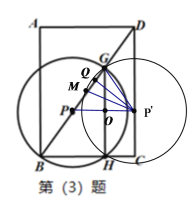
设![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广宇、承义两名同学分别进行5次射击训练,训练成绩(单位:环)如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
广宇 | 9 | 8 | 7 | 7 | 9 |
承义 | 6 | 8 | 10 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A.广宇训练成绩的平均数大于承义训练成绩平均数
B.广宇训练成绩的中位数与承义训练成绩中位数不同
C.广宇训练成绩的众数与承义训练成绩众数相同
D.广宇训练成绩比承义训练成绩更加稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户,一次性收购了![]()
![]() 小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养
小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养![]() 天的总成本为
天的总成本为![]() 万元;放养
万元;放养![]() 天的总成本为
天的总成本为![]() 万元(总成本=放养总费用+收购成本).
万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是![]() 万元,收购成本为
万元,收购成本为![]() 万元,求
万元,求![]() 和
和![]() 的值;
的值;
(2)设这批小龙虾放养![]() 天后的质量为
天后的质量为![]() (
(![]() ),销售单价为
),销售单价为![]() 元/
元/![]() .根据以往经验可知:m与t的函数关系式为
.根据以往经验可知:m与t的函数关系式为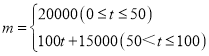 ,y与t的函数关系如图所示
,y与t的函数关系如图所示
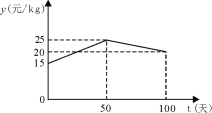
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当![]() 为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连接PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
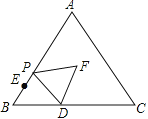
A. 8 B. 10 C. 3π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
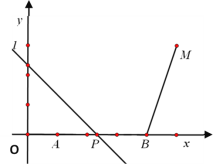
【题目】如图,点A(1, 0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y= -x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求直线l的解析式.
(2)若直线l与线段BM有公共点,求t的取值范围.
(3)当点M关于直线l的对称点落在坐标轴上时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州大学(ZhengzhouUniversity),简称“郑大”,是中华人民共和国教育部与河南省人民政府共建的全国重点大学,首批“双一流”世界一流大学、“211工程”.某学校兴趣小组3人来到郑州大学门口进行测量,如图,在大楼AC的正前方有一个舞台,舞台前的斜坡DE=4米,坡角∠DEB=41°,小红在斜坡下的点E处测得楼顶A的仰角为60°,在斜坡上的点D处测得楼顶A的仰角为45°,其中点B,C,E在同一直线上求大楼AC的高度.(结果精确到整数.参考数据:![]() ≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)
≈1.73,sin41°≈0.6,cos41°≈0.75,tan41°≈0.87)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长![]() 的标杆一端放在水渠底部的
的标杆一端放在水渠底部的![]() 点,另一端露出水面并靠在水渠边缘的
点,另一端露出水面并靠在水渠边缘的![]() 点,发现标杆有
点,发现标杆有![]() 浸没在水中,露出水面部分的标杆与水面成
浸没在水中,露出水面部分的标杆与水面成![]() 的夹角(标杆与抛物线的横截面在同一平面内).
的夹角(标杆与抛物线的横截面在同一平面内).

(1)以水面所在直线为![]() 轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
(2)在(1)的条件下,求当水面再上升![]() 时的水面宽约为多少?(
时的水面宽约为多少?(![]() 取
取![]() ,结果精确到
,结果精确到![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com