
【题目】为了了解初三学生参加体育活动的情况,某校对部分初三学生进行了调查,其中一个问题是:“你平均每天参加体育活动的时间是多少?”共有4个选项:
A.1.5小时以上 B.1—1.5小时 C.0.5—1小时 D.0.5小时以下
根据调查结果绘制了两幅不完整的统计图如下:
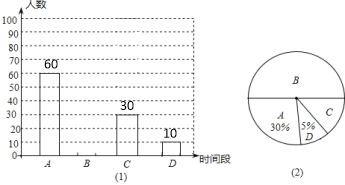
请你根据以上信息解答下列问题:
(1)本次调查的学生人数为 人,图(2)中选项C的圆心角度数为 度,请补全条形统计图。
(2)选择D选项的人中有2人来自一班,2人来自二班,学校准备从这4人中任选两人参加学校组织的师生趣味运动会,请你用列表法或画树状图的方法,求出所选的两人均来自同一个班的概率.
【答案】(1)、200,54,图形见解析;(2)、列表见解析;P=![]()
【解析】
试题分析:(1)、首先根据A的人数和百分比求出总人数;然后根据总人数求出C的百分比,从而得C的圆心角度数;根据总人数求出B的人数,从而进行补全;(2)、根据题意列出表格,从而得到概率.
试题解析:(1)、60÷30%=200(人) 30÷200×360°=54°
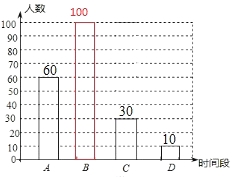
(2)、设一班的两人为A1和A2,二班的两人为B1和B2,列表可得:
A1 | A2 | B1 | B2 | |
A1 | A1,A2 | A1,B1 | A1,B2 | |
A2 | A2,A1 | A2,B1 | A2,B2 | |
B1 | B1,A1 | B1,A2 | B1,B2 | |
B2 | B2,A1 | B2,A2 | B2,B1 |
∴共12种等可能结果,其中所选的两人均来自同一个班有4种
∴P(所选两人来自同一个班)=![]()


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】为迎接G20峰会,某校开展了“手绘G20作品”美术比赛,且作品的评分只有60分,70分,80分,90分,100分这五种结果.现随机抽取其中部分作品,对其份数及成绩进行整理统计,制作如下两幅不完整的统计图.
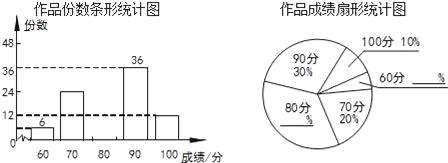
(1)本次共抽取了 份作品;
(2)其中得分为80分的作品所占的比例为 ,得分为70分的作品有 份;
(3)已知该校收到参赛的作品为1500份,估计该校学生比赛成绩达到90分以上(含90分)的作品有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x+3与直线y=-2x-1.
(1)若两直线与y轴分别交于点A,B,求点A,B的坐标;
(2)求两直线的交点C的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,连接AC,AD=2CD,点E在AD边上.
(1)如图1,若∠ECD=30°,CE=4,求△AEC的面积;
(2)如图2,延长BA至点F使得AF=2CD,连接FE并延长交CD于点G,过点D作DH⊥EG于点H,连接AH,求证:FH=![]() AH+DH;
AH+DH;
(3)如图3,将线段AE绕点A旋转一定的角度α(0°<α<360°)得到线段AE′,连接CE′,点N始终为CE′的中点,连接DN,已知CD=AE=4,直接写出DN的取值范围.
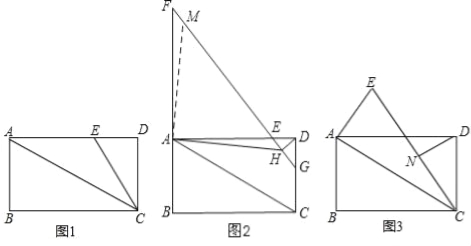
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气对北京地区的人民造成严重影响,为改善大气质量,北京市政府决定投入7600亿元治理雾霾,请你对7600亿元用科学记数法表示( )
A. 7.6×1010元B. 76×1010元C. 7.6×1011元D. 7.6×l012元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题: 如图,在数轴上点A表示的数为﹣20,点B表示的数为40,动点P从点A出发以每秒5个单位长度的速度沿正方向运动,动点Q从原点出发以每秒4个单位长度的速度沿正方向运动,动点N从点B出发以每秒8个单位的速度先沿负方向运动,到达原点后立即按原速返回,三点同时出发,当点N回到点B时,三点停止运动.![]()
(1)三个动点运动t(0<t<5)秒时,则P、Q、N三点在数轴上所表示的三个数分别为 , , .
(2)当QN=10个单位长度时,求此时点P在数轴上所表示的数.
(3)尝试借助上面数学问题的解题经验,建立数轴完成下面实际问题: 码头C位于A、B两码头之间,且知AC=20海里,AB=60海里,甲船从A码头顺流驶向B码头,乙船从C码头顺流驶向B码头,丙船从B码头开往C码头后立即调头返回B码头.已知甲船在静水中航速为5海里/小时,乙船在静水中航速为4海里/小时,丙船在静水中航速为8海里/小时,水流速度为2海里/小时,三船同时出发,每艘船都行驶到B码头停止.
在整个运动过程中,是否存某一时刻,这三艘船中的一艘恰好在另外两船之间,且与两船的距离相等?若存在,请求出此时甲船离B码头的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com