
 在△ABC中,D是CB延长线上一点,BD=AE,DE交AB于F,求证:$\frac{DF}{FE}$=$\frac{AC}{BC}$.
在△ABC中,D是CB延长线上一点,BD=AE,DE交AB于F,求证:$\frac{DF}{FE}$=$\frac{AC}{BC}$.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
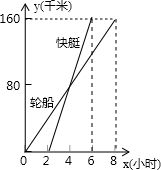 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com