
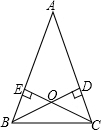
 如图,在△ABC中,AB=AC,高BD、CE相交于点O,OB与OC相等吗?请说明理由.
如图,在△ABC中,AB=AC,高BD、CE相交于点O,OB与OC相等吗?请说明理由.  培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
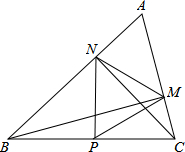 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )| A. | ①正确 | B. | ②正确 | C. | ①②都正确 | D. | ①②都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
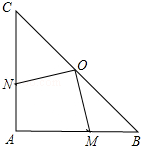 如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.
如图,在Rt△ABC中,∠A=90°,AB=AC=4cm,若O是BC的中点,动点M在AB移动,动点N在AC上移动,且AN=BM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
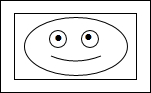 学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2.
学生会举办摄影展览,在每张长和宽分别为18厘米和12厘米的长方形相片周围镶上一圈等宽的彩纸(如图).经试验彩纸面积为相片面积的$\frac{17}{27}$时较美观,则镶在彩纸条的宽为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 2.8 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.
如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com