
【题目】对于平面内的∠MAN及其内部的一点P,设点P到直线AM,AN的距离分别为d1,d2,称![]() 和
和![]() 这两个数中较大的一个为点P关于
这两个数中较大的一个为点P关于![]() 的“偏率” . 在平面直角坐标系xOy中,
的“偏率” . 在平面直角坐标系xOy中,
(1)点M,N分别为x轴正半轴,y轴正半轴上的两个点.
①若点P的坐标为(1,5),则点P关于![]() 的“偏率”为____________;
的“偏率”为____________;
②若第一象限内点Q(a,b)关于![]() 的“偏率”为1,则a,b满足的关系为____________;
的“偏率”为1,则a,b满足的关系为____________;
(2)已知点A(4,0),B(2,![]() ),连接OB,AB,点C是线段AB上一动点(点C不与点A,B重合). 若点C关于
),连接OB,AB,点C是线段AB上一动点(点C不与点A,B重合). 若点C关于![]() 的“偏率”为2,求点C的坐标;
的“偏率”为2,求点C的坐标;
(3)点E,F分别为x轴正半轴,y轴正半轴上的两个点,动点T的坐标为(t,4),![]() 是以点T为圆心,半径为1的圆. 若
是以点T为圆心,半径为1的圆. 若![]() 上的所有点都在第一象限,且关于
上的所有点都在第一象限,且关于![]() 的“偏率”都大于
的“偏率”都大于![]() ,直接写出t的取值范围.
,直接写出t的取值范围.
【答案】(1)①5;②![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为 或
或 ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)①根据“偏率”的定义,结合点P的坐标,即可得出答案;
②根据“偏率”的定义,结合题干第一象限内点Q(a,b),即可得出答案;
(2)由点![]() ,得OB、AB长度,从而得到
,得OB、AB长度,从而得到![]() 是等边三角形.
是等边三角形.
由等边三角形性质,根据相似的判断可得![]() .则
.则![]() .
.
由于点![]() 关于
关于![]() 的“偏第”为2,所以
的“偏第”为2,所以![]() 或
或![]() .
.
再根据三角函数即可得出答案;
∴点![]() 的坐标为
的坐标为 或
或 .
.
(3)根据第(3)题意和“偏率”的定义即可得出答案.
解:(1)①5;
②![]() ;
;
(2)∵点![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,如图,
,如图,
则![]() .
.
∴![]() .
.
∴![]() .
.
∵点![]() 关于
关于![]() 的“偏第”为2,
的“偏第”为2,
∴![]() 或
或![]() .
.

当![]() 时,则
时,则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴点![]() 的坐标为
的坐标为 .
.
同理可求,当![]() 时,点
时,点![]() 的坐标为
的坐标为 .
.
∴点![]() 的坐标为
的坐标为 或
或 .
.
(3)![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
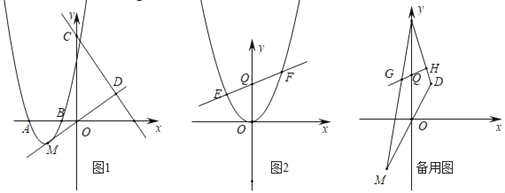
【题目】如图1,抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,抛物线的顶点为M,直线y=﹣4x+9与y轴交于点C,与直线OM交于点D.
(1)求抛物线的解析式;
(2)过Q(0,3)作不平行于x轴的直线l
①如图2,将抛物线平移,当顶点至原点时,直线l交抛物线于点E、F,在y轴上存在一点P,使△PEF的内心在y轴上,求点P的坐标;
②直线l交△CMD的边CM、CD于点G、H(G点不与M点重合、H点不与D点重合).S四边形MDHG,S△CGH分别表示四边形MDHG和△CGH的面积,试探究![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
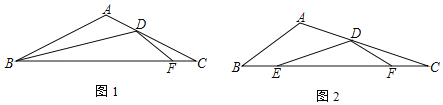
【题目】在△ABC中,点E、F在边BC上,点D在边AC上,连接ED、DF,![]() =m,∠A=∠EDF=120°
=m,∠A=∠EDF=120°
(1)如图1,点E、B重合,m=1时
①若BD平分∠ABC,求证:CD2=CFCB;
②若![]() ,则
,则![]() = ;
= ;
(2)如图2,点E、B不重合.若BE=CF,![]() =m,
=m,![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l:y=ax+b与双曲线![]() 交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
交于点A(1,m)和B(﹣2,﹣1).点A关于x轴的对称点为点C.
(1)①求k的值和点C的坐标;②求直线l的表达式;
(2)过点B作y轴的垂线与直线AC交于点D,经过点C的直线与直线BD交于点E.若30°≤∠CED≤45°,直接写出点E的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳中学为了进一步改善办学条件,决定计划拆除一部分旧校舍,建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需要800元,计划在年内拆除旧校舍与建造新校舍共9 000平方米,在实施中为扩大绿化面积,新建校舍只完成了计划的90%而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
(1)求原计划拆、建面积各是多少平方米?
(2)若绿化1平方米需要200元,那么把在实际的拆、建工程中节余的资金全部用来绿化,可绿化多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
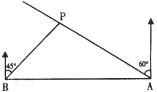
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
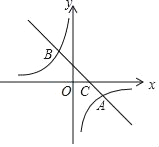
【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
(1)求k2,n的值;
(2)请直接写出不等式k1x+b<![]() 的解集;
的解集;
(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
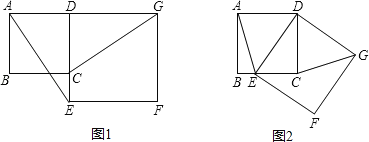
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
(1)试猜想AE与GC有怎样的关系(直接写出结论即可);
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com