
分析 分类讨论:分n=1和n≥2两种情况.依据三角形的三边关系列出方程组并解答.
解答 解:①当n=1时,1、1+$\sqrt{3}$、1+$\sqrt{3}$,能围成三角形;
②当n≥2时,由三条线段的长为$\sqrt{n}$,1+$\sqrt{n+2}$,$\sqrt{n}$+$\sqrt{n(n+2)}$,
且$\sqrt{n}$<1+$\sqrt{n+2}$<$\sqrt{n}$+$\sqrt{n(n+2)}$,
要围成三角形,需$\sqrt{n}$+1+$\sqrt{n+2}$>$\sqrt{n}$+$\sqrt{n(n+2)}$,
即$\sqrt{n(n+2)}$-$\sqrt{n+2}$<1,
$\sqrt{n+2}$($\sqrt{n}$-1)<1,
∵$\sqrt{n+2}$>$\sqrt{n}$,
∴$\sqrt{n}$($\sqrt{n}$-1)<$\sqrt{n+2}$($\sqrt{n}$-1)<1,
∴($\sqrt{n}$-$\frac{1}{2}$)2<$\frac{5}{4}$,
又∵n≥2,
∴$\sqrt{n}$-$\frac{1}{2}$>0,
∴0<$\sqrt{n}$-$\frac{1}{2}$<$\frac{\sqrt{5}}{2}$,
解得$\frac{1}{4}$<n<$\frac{\sqrt{5}+3}{2}$<3,
∴n=2,
综上所知n=1,2.
故答案为:1,2.
点评 此题考查二次根式的运用,三角形的三边关系,从简单的自然数考虑,结合数据的特点,逐步缩小n的取值得出答案即可吗.


科目:初中数学 来源: 题型:解答题
 已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.
已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
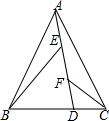 锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明.
锐角三角形△ABC中,BA=AC,过点A的直线交BC边于点D,E、F是AD上两点,∠BEA=∠AFC且∠BEA与∠AFC都与∠BAC互补,猜想EF、BE、CF之间的关系并证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
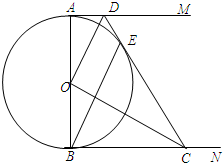 如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,
如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
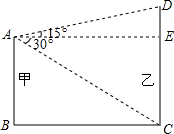 如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)
如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)2的值总是正的 | B. | a2+1的值总是正的 | ||
| C. | -(a+1)2的值总是负的 | D. | a2+1的值中,最大值是1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com