
【题目】如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A,B),过B,C,E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.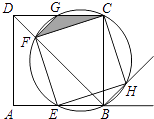
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
【答案】
(1)证明:∵B、H、C、F、E在同一圆上,且∠EBC=90°
∴∠EFC=90°,∠EHC=90°,
又∵∠FBC=∠HBC=45°,
∴CF=CH,
∵∠HBF+∠HCF=180°,
∴∠HCF=90°,
∴四边形EFCH是正方形
(2)解:∵∠BFG+∠BCG=180°,
∴∠BFG=90°,
由(1)知∠EFC=90°,
∴∠CFG+∠BFC=∠BFE+∠BFC,
∴∠CFG=∠BFE,
∴CG=BE=x,
∴DG=DC﹣CG=1﹣x,
易知△DFG是等腰直角三角形,
∴△CFG中CG边上的高为 ![]() DG=
DG= ![]() (1﹣x),
(1﹣x),
∴y= ![]() x
x ![]() (1﹣x)=﹣
(1﹣x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,y有最大值
时,y有最大值 ![]()
【解析】(1)利用圆内接四边形性质,圆周角定理,须证三个角是直角,再证一组邻边相等可得出结论;(2)利用圆内接四边形的性质可得CG=BE=x,△DFG是等腰直角三角形,利用“直角三角形斜边中线等于斜边一半”可得△CFG中CG边上的高为 ![]() DG,列出二次函数关系式,配成顶点式求出最大值.
DG,列出二次函数关系式,配成顶点式求出最大值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
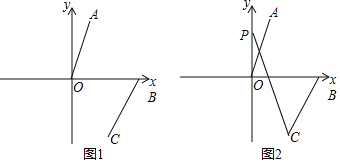
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABF中,∠F=90°,点C是线段BF上异于点B和点F的一点,连接AC,过点C作CD⊥AC交AB于点D,过点C作CE⊥AB交AB于点E,则下列说法中,错误的是( )

A.△ABC中,AB边上的高是CEB.△ABC中,BC边上的高是AF
C.△ACD中,AC边上的高是CED.△ACD中,CD边上的高是AC
查看答案和解析>>
科目:初中数学 来源: 题型:
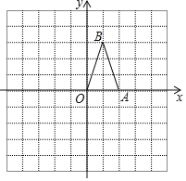
【题目】如图,在平面直角坐标系中,已知点A(2,0),点B(1,3).
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比学习)
小明同学类比除法2401615的竖式计算,想到对二次三项式x23x2进行因式分解的方法:


即x23x2x1x2,所以x23x2x1x2.
(初步应用)
小明看到了这样一道被墨水污染的因式分解题:x2□x6x2x☆,(其中□、☆代表两个被污染的系数),他列出了下列竖式:

得出□=___________,☆=_________.
(深入研究)
小明用这种方法对多项式x22x2-x-2进行因式分解,进行到了:x32x2-x-2x2*.(*代表一个多项式),请你利用前面的方法,列出竖式,将多项式x32x2-x-2因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点E为AB边上的一个动点.
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC,连结AD.试比较∠DAC与∠B的大小,并说明理由;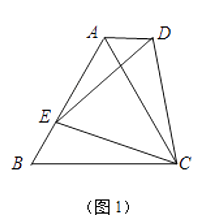
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,且△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;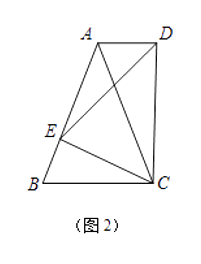
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.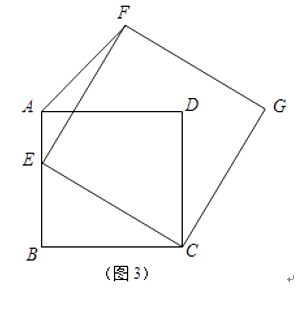
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是ABCD边上的一个动点.
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.
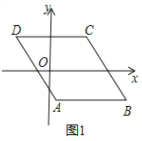
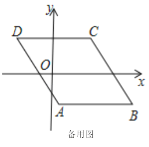
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个码头分别在一条河的两岸AC、BD上,河岸AC、BD均为东西走向,一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头,用时1.2小时,求该河的宽度(结果精确到1千米)
【参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20】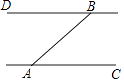
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com