
【题目】小强家有一块三角形菜地,量得两边长分别为![]() ,
,![]() ,第三边上的高为
,第三边上的高为![]() .请你帮小强计算这块菜地的面积.(结果保留根号)
.请你帮小强计算这块菜地的面积.(结果保留根号)
【答案】(600±150![]() )
)![]()
【解析】
试题本题需要分两种情况求出第三边的长度,然后计算面积.
试题解析:分两种情况:
(1)如图(1)
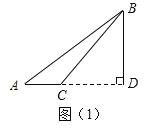
当∠ACB为钝角时,∵BD是高, ∴∠D=90°.
在Rt△BCD中,BC=40,BD=30 ∴CD=![]()
在Rt△ABD中,AB=50, ∴AD=![]() =40
=40
∴AC=AD-CD=40-10![]() ∴S=(40-10
∴S=(40-10![]() )×30÷2=(600-150
)×30÷2=(600-150![]() )
)![]()
(2)如图(2)
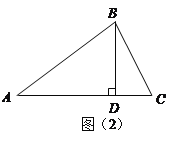
当∠ACB为锐角时,∵BD是高, ∴∠ADB=∠BDC=90°,
在Rt△BCD中,BC=40,BD=30 ∴CD=![]()
在Rt△ABD中,AB=50, ∴AD=![]() =40
=40
∴AC=AD+CD=40+10![]() ∴S=(40+10
∴S=(40+10![]() )×30÷2=(600+150
)×30÷2=(600+150![]() )
)![]()
综上所述:S= (600±150![]() )
)![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.

(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于![]() DE的同样长为半径作弧,两弧交于点F;
DE的同样长为半径作弧,两弧交于点F;
③作射线BF交AC于G.
如果BG=CG,∠A=60°,那么∠ACB的度数为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
在数轴上4与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]()
在数轴上![]() 与3所对的两点之间的距离
与3所对的两点之间的距离![]() ;
;
在数轴上![]() 与
与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() 在数轴上点A、B分别表示数a、b,则A、B两点之间的距离
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离![]()
依据材料知识解答下列问题
![]() 数轴上表示
数轴上表示![]() 和
和![]() 的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
![]() 七年级研究性学习小组进行如下探究:
七年级研究性学习小组进行如下探究:
![]() 请你在草稿纸上面出数轴当表示数x的点在
请你在草稿纸上面出数轴当表示数x的点在![]() 与2之间移动时,
与2之间移动时,![]() 的值总是一个固定的值为:______,式子
的值总是一个固定的值为:______,式子![]() 的最小值是______.
的最小值是______.
![]() 请你在草稿纸上画出数轴,当x等于______时,
请你在草稿纸上画出数轴,当x等于______时,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.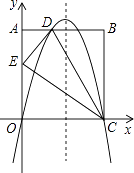
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com