
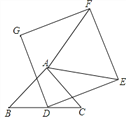
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,连接AE,若BC=DE=2,将正方形DEFG绕点D逆时针方向旋转,在旋转过程中,当AE为最大值时,则AF的值_____________.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
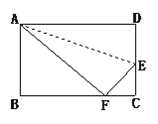
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).此时EC有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出图所示的统计图,已知图中从左到右的四个长方形的高的比为:14:9:6:1,评价结果为D等级的有2人,请你回答以下问题: ①共抽测了人;②样本中B等级的频率是;
③如果要绘制扇形统计图,D等级在扇形统计图中所占的圆心角是度;
④该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有名学生可以报考示范性高中.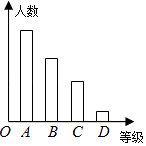
查看答案和解析>>
科目:初中数学 来源: 题型:
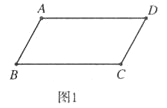
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二 次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四 边形ABCD为1阶准菱形.
(I)判断与推理:
(i)邻边长分别为2和3的平行四边形是_________阶准菱形;
(ii)为了剪去一个菱形,进行如下操作:如图2,把平行四边形ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE,请证明四边形ABFE是菱形.
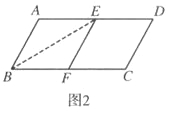
(Ⅱ)操作与计算:
已知平行四边形ABCD的邻边长分别为l,a(a>1),且是3阶准菱形,请画出平行四边形ABCD及裁剪线的示意图,并在图形下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在直角坐标系中,有A(0,3),B(2,1),C(﹣3,﹣3)三点.
(1)请在平面直角坐标系中描出各点,并画出三角形ABC;
(2)三角形ABC的面积是 ;(直接写出结果)
(3)设BC交y轴于点P,试求P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,过点A作直线EF. 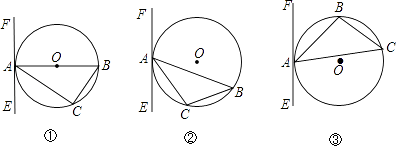
(1)如图①,AB为直径,要使EF为⊙O的切线,还需添加的条件是(只需写出三种情况): ①;②;③ .
(2)如图②,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线.
(3)如图③,AB是非直径的弦,∠CAE=∠ABC,EF还是⊙O的切线吗?若是,请说明理由;若不是,请解释原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 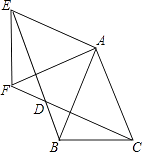
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com