
【题目】已知二次函数![]()
![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为Rt△ABC的斜边,∠CBA=30°,△ABD,△ACF,△BCE均为正三角形,四边形MNPE是长方形,点F在MN上,点D在NP上,若AC=2,则图中空白部分的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题
数学课上,老师出示了这样一道题:如图,![]() 中,
中,![]() ,点P为边AB上一点(不与A、B重合),过P作
,点P为边AB上一点(不与A、B重合),过P作![]() 于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段
于Q,做QE∥AB交BC于点E,连接PE,将线段PE绕点P顺时针旋转90°到PF,连接QF,探究线段![]() 之间的数量关系并证明.
之间的数量关系并证明.
同学们经过思考后,交流了自已的想法
小明:“通过观察和度量,发现![]() 为直角.”
为直角.”
小伟:“我通过一线三直角的模型构造三角形全等可以解决问题.”
小强:“我构造等腰直角三角形,再利用全等三角形可以解决问题.”
老师:“若其他条件不变,PE=![]() AC,就可以求出
AC,就可以求出![]() 的值.”
的值.”
(1)![]() 多少度?四边形
多少度?四边形![]() 为什么特殊四边形?(直接写出答案)
为什么特殊四边形?(直接写出答案)
(2)探究线段![]() 之间的数量关系并证明;
之间的数量关系并证明;
(3)若其他条件不变,PE=![]() AC,求
AC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
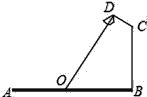
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
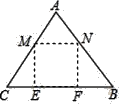
【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2![]() 2x+c的顶点A在直线l:y=x
2x+c的顶点A在直线l:y=x![]() 5上.
5上.
(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)在直线l上是否存在一点P,使以点P、A、B、D为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com