
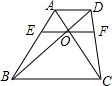
 如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )
如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )| A. | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | C. | $\frac{AE}{AB}$=$\frac{DO}{BO}$ | D. | $\frac{CD}{CF}$=$\frac{BD}{BO}$ |
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
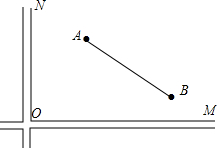 如图,在两条相互垂直的高速公路0M、0N旁有两个相距50km的风景区A和B,A、B到0M的距离分别为40kn和10km,A到0N的距离为30km,现打算在0M旁和0N旁各修建一服务区C、D,使A、B、C、D构成的四边形的周长最小,求出这个最小值(高速公路的宽忽略不计).
如图,在两条相互垂直的高速公路0M、0N旁有两个相距50km的风景区A和B,A、B到0M的距离分别为40kn和10km,A到0N的距离为30km,现打算在0M旁和0N旁各修建一服务区C、D,使A、B、C、D构成的四边形的周长最小,求出这个最小值(高速公路的宽忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
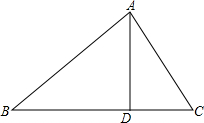 有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米?
有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com