【答案】
分析:(1)根据MC的函数式不难得出C点的坐标应该是(0,-3),即c=-3,那么要求抛物线的解析式还缺少一个点的坐标,可根据OC=3,以及∠BCO的余弦值在直角三角形BCO中运用勾股定理求出OB的长,也就得出了B的坐标,进而可求出抛物线的解析式.
(2)假设存在这样的点P,那么要分两种情况进行讨论:
①当PN是另外一条直角边时,可先求出直线MC的函数解析式,然后确定出N点的坐标,如果PN与y轴的交点为N,那么直角三角形CND应该是个等腰直角三角形(∠OCN=45°),因此可求出OD的长,也就得出了D的坐标,然后可确定出直线PN的解析式,然后联立抛物线和PN所在直线的解析式即可求出此时交点P的坐标.
②当PC是另外一条直角边时,连接AC可发现,AC⊥CN(∠ACO=∠NCO=45°),而C点又正好在抛物线上,因此P与A重合,那么P点的坐标就是A点的坐标.
(3)①先求上移的单位,可先设出平移后的二次函数的解析式,然后联立抛物线和直线NQ即MC的解析式,然后可得出一个一元二次方程,要想使两函数有交点,那么△≥0,以此可求出平移单位的取值范围,也就可求出最大的平移值.
②要求向下平移的最大单位,可求出当Q,N正好在抛物线上时,b的取值,那么根据MC的直线解析式,可得出Q,N点的坐标,那么当Q,N正好在抛物线上时,可用Q,N得出b的值,然后即可求出向下平移的最大单位.
解答: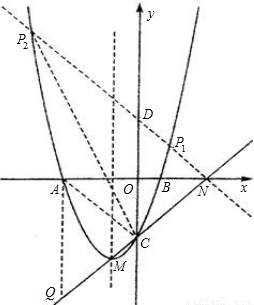
解:(1)∵直线MC的函数表达式y=kx-3.
∴点C(0,-3)
∴cos∠BCO=
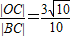
=
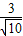
∴可设|OC|=3t(t>0),|BC|=
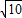
t
则由勾股定理,得|OB|=t
而|OC|=3t=3,
∴t=1
∴|OB|=1,
∴点B(1,0)
∵点B(1,0)C(0,-3)在抛物线上
∴
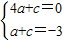
,
解得
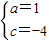
,
∴抛物线的函数表达式为y=(x+1)
2-4=x
2+2x-3.
(2)假设在抛物线上存在异于点C的点P,使以N,P,C为顶点的三角形是以NC为一条直角边的直角三角形,
①若PN为另一条直角边
∵点M(-1,-4)在直线MC上,
∴-4=-k-3,即k=1
∴直线MC的函数表达式为y=x-3
易得直线MC与x轴的交点N的坐标为N(3,0)
∵|OC|=|ON|
∴∠CNO=45°
∴在y轴上取点D(0,3),
连接ND交抛物线于点P
∵|ON|=|OD|
∴∠DNO=45°
设直线ND的函数表达式为y=mx+n
由
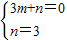
得
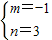
∴直线ND的函数表达式为y=-x+3
设点P(x,-x+3),代入抛物线的函数表达式,
得-x+3=x
2+2x-3,
即x
2+3x-6=0
解得x
1=
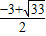
,x
2=
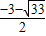
∴y
1=
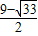
,y
2=
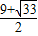
∴满足条件的点为P
1(
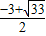
,
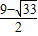
),p
2(
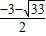
,
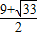
).
②若PC是另外一条直角边
∵点A是抛物线与x轴的另一交点,
∴点A的坐标为(-3,0)
连接AC,∵|OA|=|OC|,
∴∠OCA=45°,又∠OCN=45°
∴∠ACN=90°,
∴点A就是所求的点p
3(-3,0)
综上所述,在抛物线上存在满足条件的点,有3个,
分别为:P
1(
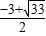
,
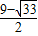
),p
2(
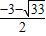
,

),p
3(-3,0).
(3)若抛物线沿其对称轴向上平移,
设向上平移b(b>0)个单位可设函数表达式为y=x
2+2x-3+b
由
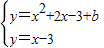
,
得x
2+x+b=0.
∴要使抛物线与线段NQ总有交点,
必须△=1-4b≥0,即b≤

,
∴0<b≤

∴若抛物线向上平移,最多可平移

个单位长度.
②若抛物线沿其对称轴向下平移,设向下平移b(b>0)个单位
可设函数表达式为y=x
2+2x-3-b
∵当x=-3时,y=-b,当x=3时,y=12-b
易求得Q(-3,-6),又N(3,0)
∴要使抛物线与线段NQ总有交点,必须
-b≥-6或12-b≥0,即b≤6或b≤12
∴0<b≤12
∴若抛物线沿其对称轴向下平移,最多可平移12个单位长度
综上可知,若抛物线沿其对称轴向下平移,使抛物线与线段NQ总有公共点,
则向上最多可平移

个单位长度,向下最多可平移12个单位长度.
点评:本题的关键是在于根据已知条件确定二次函数的解析式以及二次函数平移后解析式的变化情况,
要注意的是(2)中要分另一条直角边的不同进行分类讨论,不要漏解.

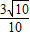 .
. 解:(1)∵直线MC的函数表达式y=kx-3.
解:(1)∵直线MC的函数表达式y=kx-3.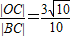 =
=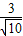
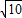 t
t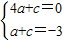 ,
,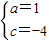 ,
,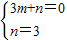
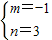
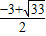 ,x2=
,x2=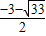
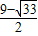 ,y2=
,y2=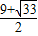
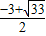 ,
,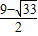 ),p2(
),p2(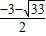 ,
,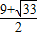 ).
).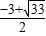 ,
,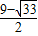 ),p2(
),p2(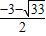 ,
, ),p3(-3,0).
),p3(-3,0).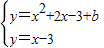 ,
, ,
,
 个单位长度.
个单位长度. 个单位长度,向下最多可平移12个单位长度.
个单位长度,向下最多可平移12个单位长度.

 阅读快车系列答案
阅读快车系列答案 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为