
����Ŀ������ijһ�����������¶��壺��������ʵ��![]() �����Ա���
�����Ա���![]() ʱ������
ʱ������![]() ����
����![]() �ĺ���ͼ��Ϊ
�ĺ���ͼ��Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ۺ�õ��ĺ���ͼ��Ϊ
���ۺ�õ��ĺ���ͼ��Ϊ![]() ������
������![]() ��ͼ����
��ͼ����![]() ��
��![]() �����ֹ�ͬ��ɣ�����
�����ֹ�ͬ��ɣ�����![]() Ϊԭ�����������ۺ��������纯��
Ϊԭ�����������ۺ��������纯��![]() (
(![]() )�Ķ��ۺ���Ϊ
)�Ķ��ۺ���Ϊ![]() .
.
(1)����![]() (
(![]() )�Ķ��ۺ�����
)�Ķ��ۺ�����
(2)����![]() �ں���
�ں���![]() (
(![]() )�Ķ��ۺ�����ͼ���ϣ���
)�Ķ��ۺ�����ͼ���ϣ���![]() ��ֵ��
��ֵ��
(3)������![]() (
(![]() )�Ķ��ۺ�����
)�Ķ��ۺ�����![]() ���в�ͬ�Ľ������ʱ��ֱ��д��
���в�ͬ�Ľ������ʱ��ֱ��д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
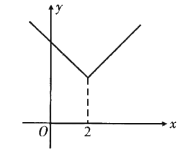
���𰸡�(1)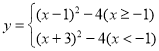 ��(2)
��(2)![]() ��-6��(3)n<-1ʱ����x����4�����㣬n=-1ʱ����x����3�����㣻
��-6��(3)n<-1ʱ����x����4�����㣬n=-1ʱ����x����3�����㣻![]() ��x����2�����㣻n=3ʱ����x����3�����㣻n>3ʱ����x������.
��x����2�����㣻n=3ʱ����x����3�����㣻n>3ʱ����x������.
��������
��1�����ݶ���ó����ۺ����Ķ�������Ϊ![]() ���ú�������ʽΪ��
���ú�������ʽΪ��![]() ��
��
��2������![]() ����
���� ����m��ֵ���ɣ�
����m��ֵ���ɣ�
��3��)�ֵ�![]() ʱ����
ʱ����![]() ʱ�� ��
ʱ�� ��![]() ʱ����
ʱ����![]() ʱ����
ʱ����![]() ʱ����������ĺ���ͼ����й۲���x��Ľ����������
ʱ����������ĺ���ͼ����й۲���x��Ľ����������
(1)��![]() ����
����![]() ��3����ͼ1������
��3����ͼ1������![]() ������Ϊ
������Ϊ![]() ��
��![]() ������ۺ����Ķ�������Ϊ
������ۺ����Ķ�������Ϊ![]() ���ú�������ʽΪ��
���ú�������ʽΪ��![]() ��
��
�����ۺ���Ϊ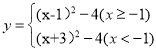 .
.
(2)����![]() ����
����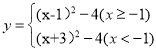
��ã�![]() ��-6(���������ֵ����ȥ)
��-6(���������ֵ����ȥ)
��![]() ��-6��
��-6��
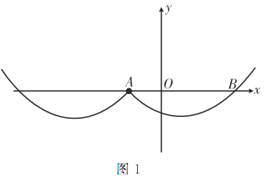
(3)�ٵ�![]() ʱ����ͼ2��
ʱ����ͼ2��
��ʱ![]() �ڵ�
�ڵ�![]() ����࣬��ͼ�п��Կ�����������
����࣬��ͼ�п��Կ�����������![]() ����4������
����4������![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ����
����![]() ����ͼ1���Կ�����������
����ͼ1���Կ�����������![]() ����3�����㣻
����3�����㣻
��ͬ������![]() ʱ��������
ʱ��������![]() ����2�����㣻
����2�����㣻
��ͬ������![]() ʱ��������
ʱ��������![]() ����3�����㣻
����3�����㣻
��ͬ������![]() ʱ������.
ʱ������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
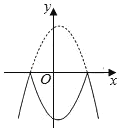
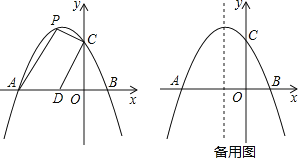
����Ŀ����ͼ����������y=x2+2x+8��ͼ��x���Ϸ��IJ�����x���۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ����ͼ��(ʵ�߲���)����P(a��ka-1)�ڸú����ϣ��������ĵ�Pǡ����3������k��ֵΪ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+2��x���ڵ�A(-3��0)�͵�B(1��0)����y���ڵ�C��
(1)����������ߵĺ�������ʽ��
(2)��D������Ϊ(-1��0)����PΪ�ڶ��������������ϵ�һ�����㣬���ı���ADCP��������ֵ��
(3)��MΪ�����߶Գ����ϵĵ㣬�ʣ������������Ƿ���ڵ�N��ʹ��MNOΪ����ֱ�������Σ��ҡ�MNOΪֱ�ǣ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵ����ߣ���E��AD���е㣬����A��AF��BC��BE���ӳ�����F������CF��
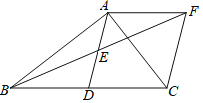
��1����֤����AEF�ա�DEB��
��2������BAC=90�������ж��ı���ADCF����״����֤����Ľ��ۣ�
��3���ڣ�2��������£���M��AC�߶����ƶ�����ֱ�ӻش𣬵���M�ƶ���ʲôλ��ʱ��MB+MD����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��2x��1��
x | �� | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | �� �� | �� �� | �� �� | �� �� | �� �� | �� |
��1�����ڱ��ڵĿո��������ʵ�������
��2�������б�������������ƽ��ֱ������ϵ�л���y=x2��2x��1��ͼ��
��3����x��ʲô��Χ��ʱ��y��x�������С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD����A=60����AB=6����E��F�ֱ���AB��BC������ijһ�����˶��ĵ㣬��DE=DF������E��A�˶���Bʱ���߶�EF���е�O�˶���·��Ϊ_____.
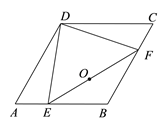
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�a+1��x2+2bx+��a+1����0��������ȵ�ʵ������������˵����ȷ���ǣ�������
A. 1һ�����Ƿ���x2+bx+a��0�ĸ�B. 0һ�����Ƿ���x2+bx+a��0�ĸ�
C. ��1�����Ƿ���x2+bx+a��0�ĸ�D. 1�ͩ�1���Ƿ���x2+bx+a��0�ĸ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������ɻ��£�AB�Σ��ͻ������BC�Σ���ɣ���ͼ��ʾ����ѩ���ڻ����ϻ��еľ���y����λ��m���ͻ���ʱ��t1����λ��s��������κ�����ϵ�������������ݣ�
����ʱ��t1/s | 0 | 1 | 2 | 3 | 4 |
�����y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
��ѩ���ڻ�����ϻ��еľ���y2����λ��m�����ڻ�����ϻ���ʱ��t2����λ��s�����㣺y2��52t2��2t22����ѩ�ߴ�A�����ڻ����BC��ֹͣ��һ������23s������AB�ij��ȣ���������
A.270B.280C.375D.450
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
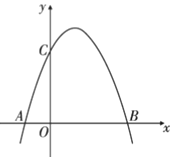
����Ŀ����ͼ����֪������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() �͵�
�͵�![]() (��
(��![]() �ڵ�
�ڵ�![]() �����)����
�����)����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() .
.
(1)���![]() �͵�
�͵�![]() �����ꣻ
�����ꣻ
(2)����![]() Ϊ��������һ�㣬��
Ϊ��������һ�㣬��![]() �����
�����![]() ������.
������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com