
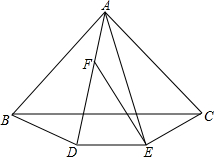
 如图,△ABD、△ADE、△AEC都是顶角为30°的等腰三角形,∠AEF=15°,AF=1,则BD=$\sqrt{2}$.
如图,△ABD、△ADE、△AEC都是顶角为30°的等腰三角形,∠AEF=15°,AF=1,则BD=$\sqrt{2}$. 分析 作FG⊥AE于G,作DH⊥EF于H,则∠DHE=∠DHF=∠AGF=∠EGF=90°,由已知条件得出BD=DE,AD=AE,∠AED=75°,GF=$\frac{1}{2}$AF=$\frac{1}{2}$,再证出∠EDH=30°,△DHF是等腰直角三角形,得出DE=2EH,DH=$\sqrt{3}$EH,FH=DH,设EH=x,则BD=DE=2x,FH=DH=$\sqrt{3}$x,得出DF=$\sqrt{2}$DH=$\sqrt{6}$x,EF=$\sqrt{3}$x+x,AE=AD=$\sqrt{6}$x+1,在Rt△EFG中,根据勾股定理得出方程,解方程求出x,即可得出BD.
解答 解:作FG⊥AE于G,作DH⊥EF于H,如图所示:
则∠DHE=∠DHF=∠AGF=∠EGF=90°,
∵△ABD、△ADE、△AEC都是顶角为30°的等腰三角形,
∴BD=DE,AD=AE,∠AED=75°,GF=$\frac{1}{2}$AF=$\frac{1}{2}$,
∴AG=$\sqrt{3}$GF=$\frac{\sqrt{3}}{2}$,
∵∠AEF=15°,
∴∠DEF=75°-15°=60°,∠DFE=30°+15°=45°,
∴∠EDH=30°,△DHF是等腰直角三角形,
∴DE=2EH,DH=$\sqrt{3}$EH,FH=DH,
设EH=x,则BD=DE=2x,FH=DH=$\sqrt{3}$x,
∴DF=$\sqrt{2}$DH=$\sqrt{6}$x,EF=$\sqrt{3}$x+x,AE=AD=$\sqrt{6}$x+1,
在Rt△EFG中,根据勾股定理得:GF2+GE2=EF2,
即($\frac{1}{2}$)2+($\sqrt{6}$x+1-$\frac{\sqrt{3}}{2}$)2=($\sqrt{3}$x+x)2,
解得:x=$\frac{\sqrt{2}}{2}$,
∴BD=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$;
故答案为:$\sqrt{2}$.
点评 本题考查了勾股定理、等腰三角形的性质、含30°角的直角三角形的性质、等腰直角三角形的判定与性质、三角函数等知识;本题综合性强,难度较大,需要通过作辅助线运用三角函数和勾股定理得出方程才能得出结果.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com