
 如图,在9×10的正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
如图,在9×10的正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.| AC |
| DC |
| BC |
| CE |
| AC |
| DC |
| 3 |
| 2 |
| BC |
| CE |
| 6 |
| 4 |
| 3 |
| 2 |
| AC |
| DC |
| BC |
| CE |


科目:初中数学 来源: 题型:
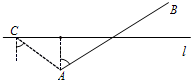 于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.
于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
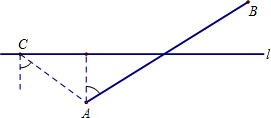
查看答案和解析>>
科目:初中数学 来源: 题型:
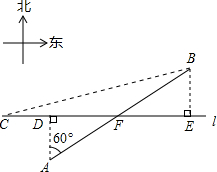 (2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.
(2013•崇明县一模)如图,在航线l的两侧分别有观测点A和B,点A到航线l的距离为2海里,点B位于点A北偏东60°方向且与A相距l0海里处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,10分钟后该轮船行至点A的正北方向的D处.| 3 |
查看答案和解析>>
科目:初中数学 来源:2011年浙江省宁波市外贸学校中考模拟数学卷 题型:解答题
如图,在航线L的两侧分别有观测点A和B,点A到航线L的距离为2km,点B位于点A北偏东60°方向且与A相距5km处。现有一艘轮船正沿该航线自西向东航行,在C点观测到点A位于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向。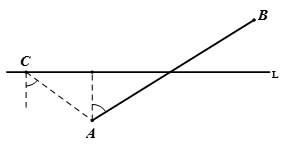
【小题1】(1)求观测点B到航线L的距离;
【小题2】(2)求该轮船航线的速度(结果精确到0.1km/h,参考数据: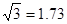 ,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
,sin54°="0.81 " cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源:2011年浙江省宁波市外贸学校中考模拟数学卷 题型:解答题
如图,在航线L的两侧分别有观测点A和B,点A到航线L的距离为2km,点B位于点A北偏东60°方向且与A相距5km处。现有一艘轮船正沿该航线自西向东航行,在C点观测到点A位于南偏东54°方向,航行10分钟后,在D点观测到点B位于北偏东70°方向。
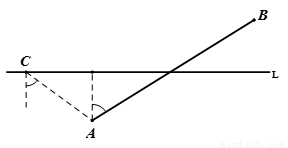
1.(1)求观测点B到航线L的距离;
2.(2)求该轮船航线的速度(结果精确到0.1km/h,参考数据: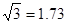 ,sin54°=0.81 cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
,sin54°=0.81 cos54°=0.59,tan54°=1.38,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com